Have you heard of 1+1=1? That may be incorrect in terms of Math, but not in certain situations. Say that you have two images: a photo of a mountain and a sun. If you put the sun's image on top of the mountain image, you'll get a new picture with both the mountain and the sun. If you've worked with creative software, this is similar to layering.
Likewise, structures behave that way. One similar model added to another one will give you a new structure! That is the idea of superposition. Based on that, it implies the following possibilities:
- We can add reactions, internal forces, and deflection of similar structures with different loading conditions to get a new structure with combined effects.
- Break down an existing structure into similar ones that we can combine again. We can analyze these independent structures by themselves.
In summary, superposition tells us that the effect of one point in a structure due to various loads acting on it is the sum when these loads work separately. It is a powerful concept in structural analysis. Later in this course, we'll see how we can use it to analyze complex trusses, deflections, and indeterminate structures.
It is also essential to take note that structures must be similar. Superposition works if the structures are identical in type, geometry, shape, and rigidity at corresponding points. In addition, superposition only works if models behave linearly.
Example
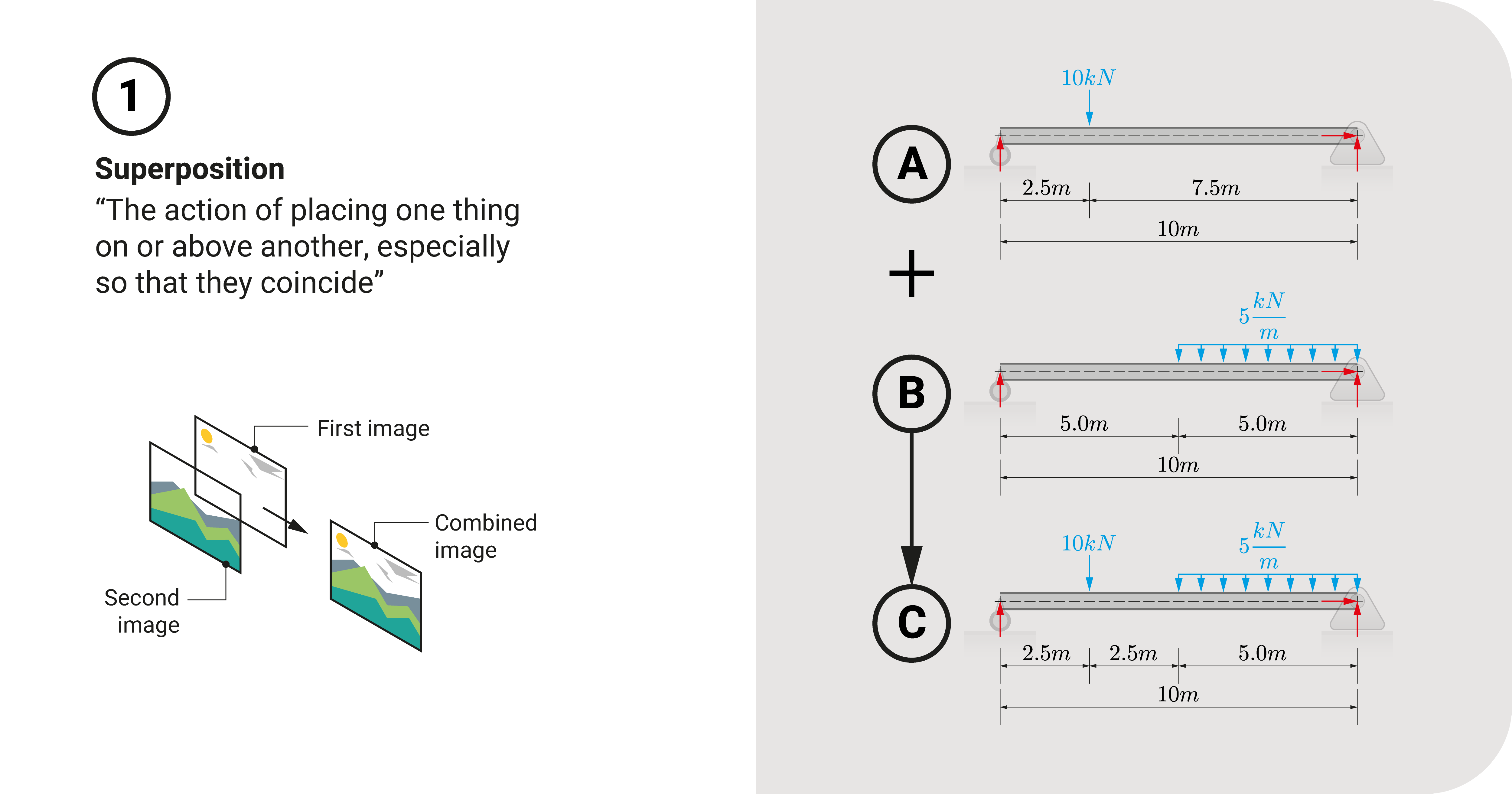
To best explain this concept, let's investigate two beams. These structures have the same longitudinal and cross-sectional properties (flexural rigidity is assumed to be \(1\times{10}^{12}\) for illustration purposes). The first beam consists of a \(10kN\) load applied \(2.5m\) from the left support. The second beam consists of a \(5kN/m\) uniformly distributed load from \((5,0)\) to \((10,0)\).
Below are their shear \(V\), moment \(M\), slope \(\theta\), and deflection \(\Delta\) diagrams (you can interact with these graphs!).
Beam A
Beam B
Now, suppose you add the loadings conditions, \(V\), \(M\), \(\theta\), and \(\Delta\) at similar points for both members. In that case, you'll arrive at a third beam similar in length \(L\) and material properties \((E, I)\) of the last two beams; As a consequence, the effects of the third beam should be the same if you are to analyze it by itself.
Beam C - Superimposed Beam
For example, let's add the shear at the right end of these two beams, which are \(-2.50 kN\) and \(-18.8 kN\), respectively. With superposition, the shear at the right end \(V\) of the third beam is equal to \(-21.25 kN\). It should be the same result if you analyze the third beam alone.
Summary
Superposition allows you to add reactions, internal forces, and deflection of similar structures with different loading conditions to get a combined similar structure.
Superposition implies we can "break down" an existing structure into similar structures that can be combined again.
We use superposition to analyze complex trusses, deflections, and indeterminate structures, to name a few.
Structures must be similar for superposition to work.
Structures must behave linearly for this principle to work.






