In structural analysis, some methods will use work and energy concepts. This article is a refresher on those ideas.
What is Work?
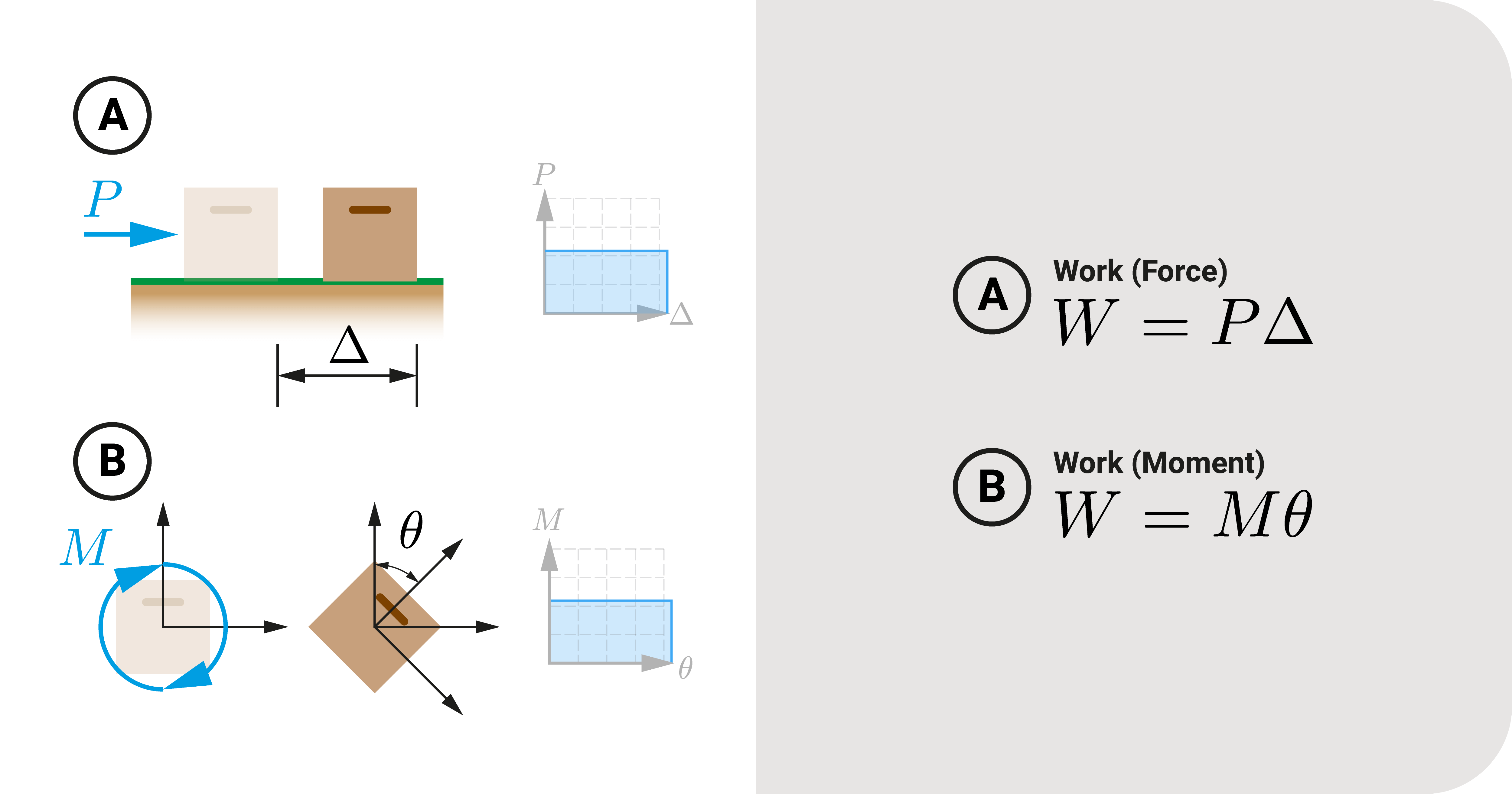
At its simplest, work \(W\) happens if a force or moment causes something to move. It is a scalar product of force \(P\) and displacement \({\Delta}\) or moment \(M\) and rotation \({\theta}\): \(W=P{\times}{\Delta}\) or \(W=M{\times}{\theta}\)
The basic unit of work is the Joule \(J\), equivalent to \(1 N•m\). Graphically speaking, work is the area under a \(P-∆\) or \(M-θ\) graph.
Must Be In Same Line of Action!
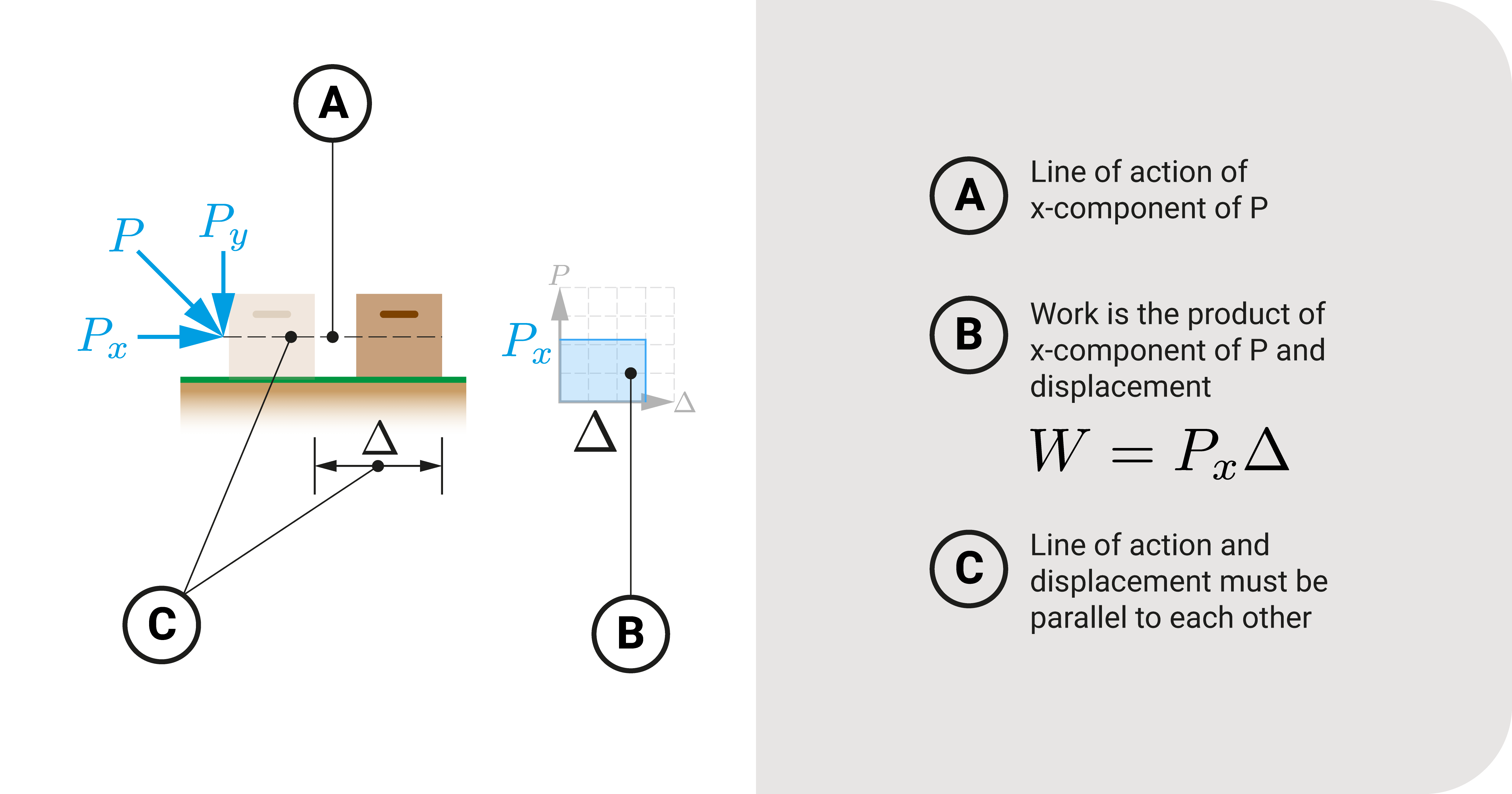
In addition to our basic definitions, work only exists if \(F\) and \(∆\) or \(M\) and \(θ\) are acting in the same path.
To illustrate, consider an object, say a box. We apply a pushing force \(P\) on it.
- Force \(P\) can be broken down to its components along the \(x\) and \(y\)-axes: \(P_x\) and \(P_y\) respectively.
- There is work done with \(P_x\) and \({\Delta}\) because \(P_x\) and \({\Delta}\) act in the same line which is the \(+x\)-axis (parallel to each other); however,
- there is no work done with \(P_y\) and \({\Delta}\) because the paths are perpendicular to each other.
The same is valid with rotation, \(M\) and \({\theta}\) must be acting on the same line of action to have work.
Positive and Negative Work
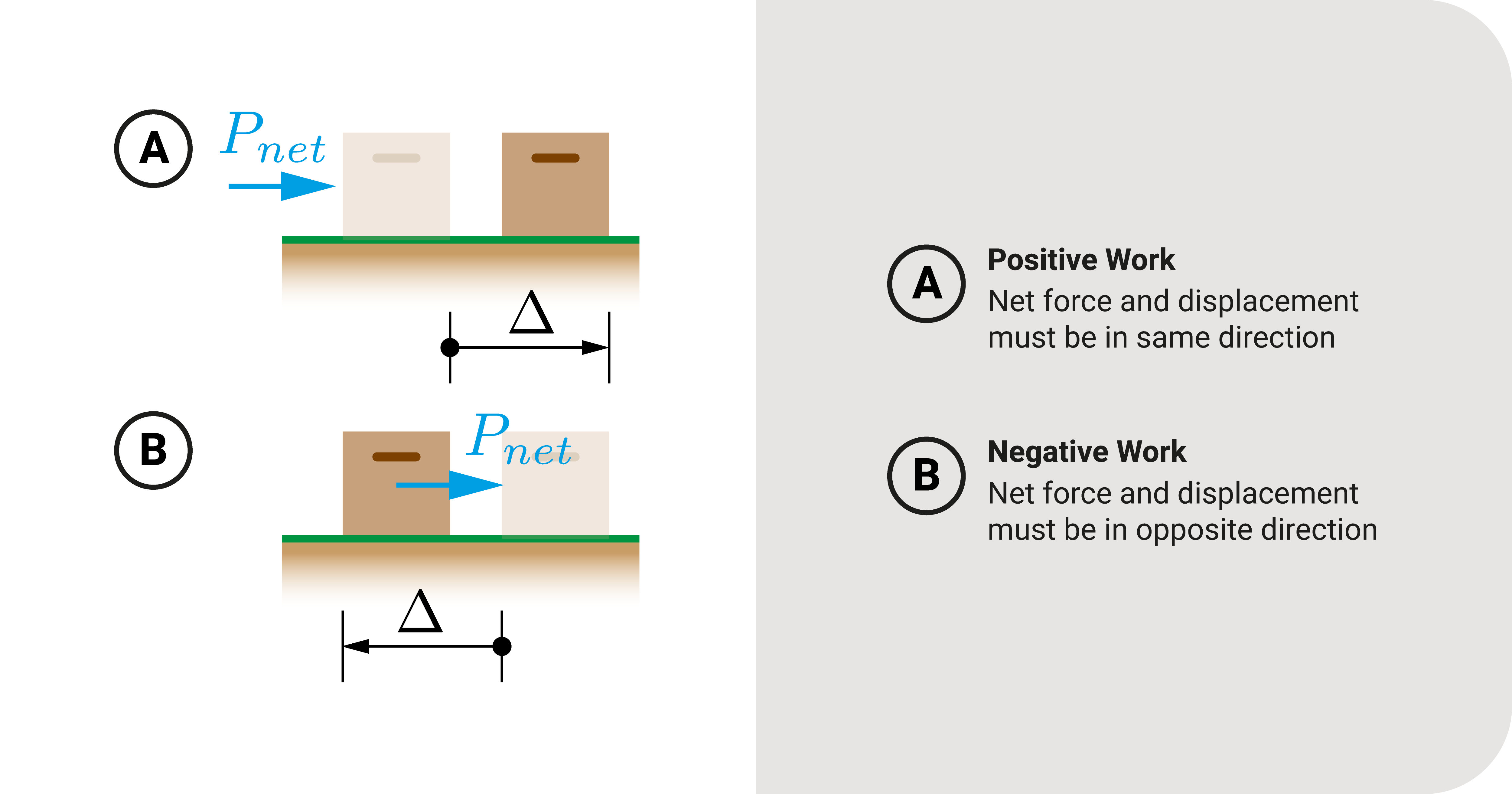
In addition, work can either be positive or negative:
- Work is positive if the net force (or net moment) has the same direction as the displacement (or rotation).
- It is negative if the net force (or net moment) and displacement (or rotation) are opposite.
Total Work or Net Work
Given a body, many forces may act on it. As such, these forces may perform multiple work on it (either positive or negative). The algebraic sum of all these work on the body is what we call total work \(W_{tot}\).
\(W_{tot}={\sum}W\)
Virtual Work
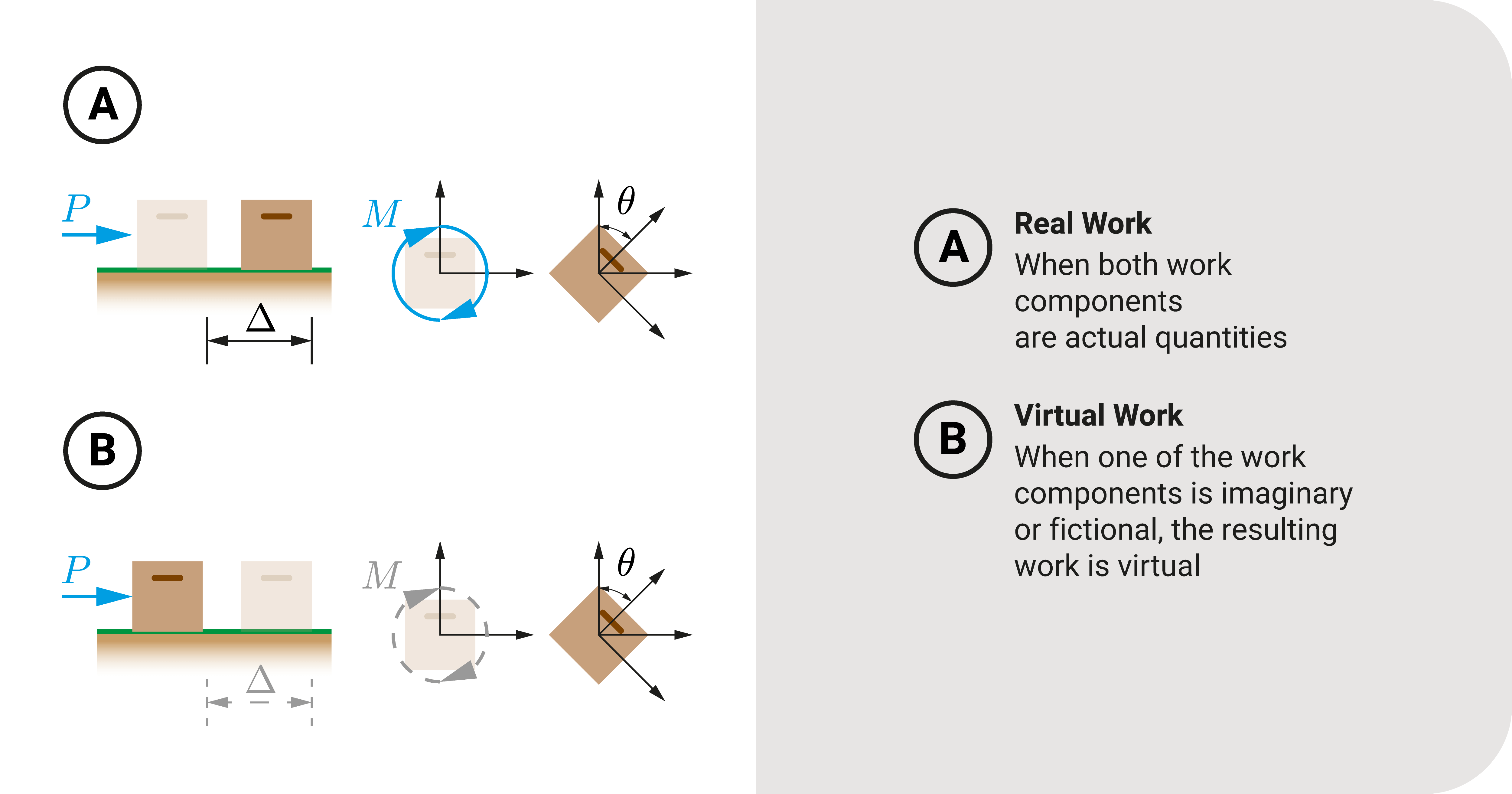
We said that work is \(W=P{\times}{\Delta}\) or \(W=M{\times}{\theta}\). If both of these quantities are actual, we call this real work.
However, if either is an imaginary quantity, we call it virtual work. As such, there are two possible instances in which there is virtual work:
- Real force \(P\) times fictional displacement \(\Delta\), or real moment \(M\) times imaginary rotation \(\theta\).
- Imaginary force \(P\) times actual displacement \(\Delta\), or fictional moment \(M\) times actual rotation \(\theta\).
What is Energy?
Let's now move on to a related term, energy, which is the ability to do work.
Work and energy are related and sometimes interchangeable concepts. These scalar quantities have the same SI unit (Joule, \(J\)).
The difference is that work happens if some external force causes movement, while energy is inherent in an object or system. For example, we say a battery has "chemical energy "instead of "chemical work" because it is natural for such a thing to have.
Potential and Kinetic Energy
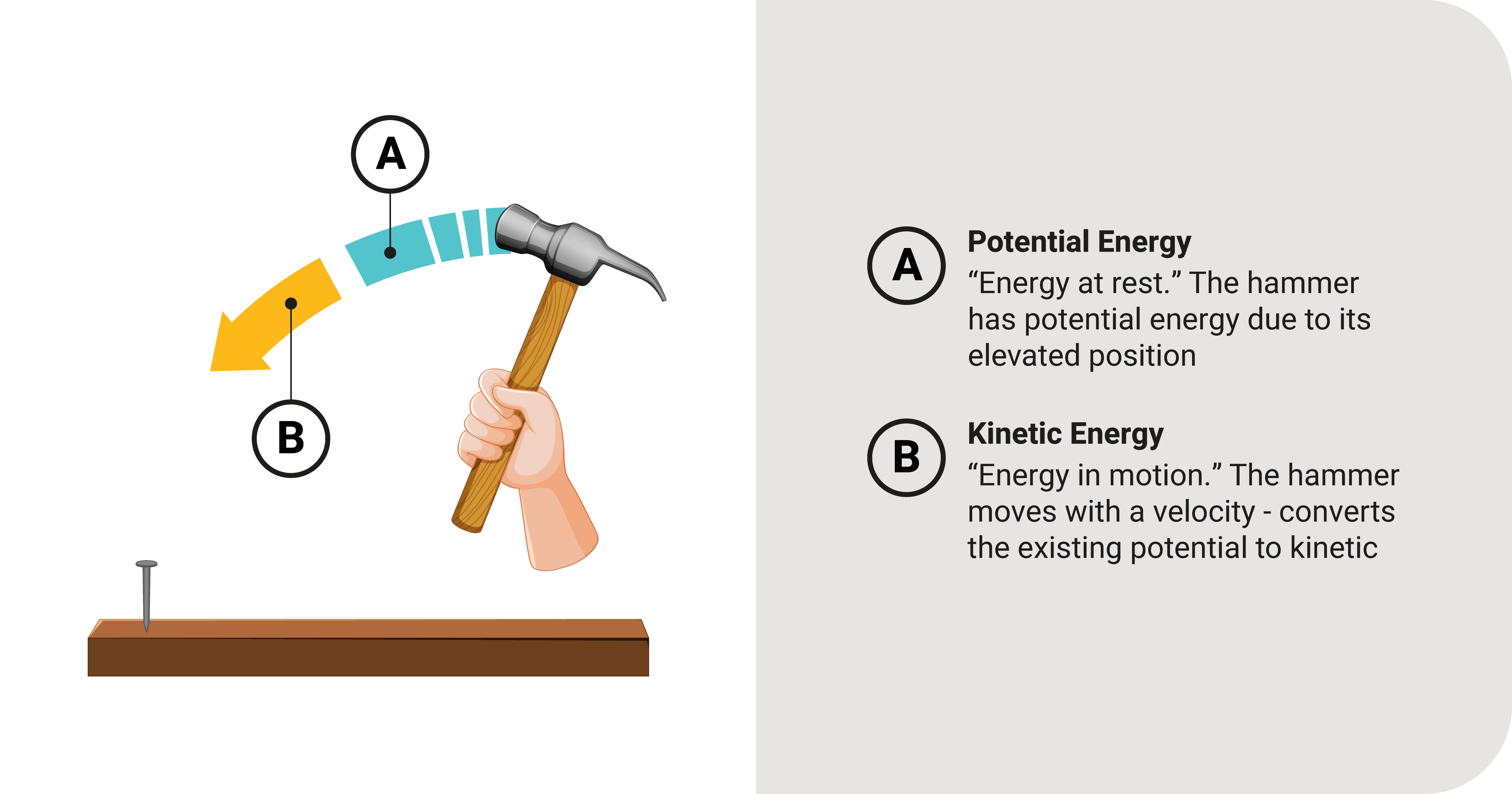
There are two general categories of energy: potential \(U\) and kinetic energy \(K\); The former deals with "energy at rest," or due to its position, while the latter is "energy in motion."
Potential energy has many forms. Example include gravitational \(U_g\), elastic \(U_e\), and chemical \(U_c\). Each of these types deserves a separate discussion.
Kinetic energy is the amount of work needed to bring an object of mass \(m\) from rest to a speed of \(V\). Equation-wise, \(K\) is:
\(K=\frac{1}{2}mV^2\)
Energy Forms

We can also express energy in different forms depending on the source and nature of things. As a taste, here are some examples:
- Mechanical Energy is the sum of potential and kinetic energy on a visible scale.
- Strain Energy is potential energy due to the deformation of an object.
- Thermal Energy is kinetic energy due to the microscopic motion of particles.
Work-Energy Theorem
The total work \(W_{tot}\) on a body is related to two things: (1) the displacement and (2) the speed of the body. We can see these relationships in the work-energy theorem.
Given the kinetic energy of a body before and after its movement as \(K_1\) and \(K_2\) and the total work done \(W_{tot}\), the work-energy states that:
\(W_{tot}=\Delta{K}=K_2-K_1\)
The change in kinetic energy equals the total work done on the body.
Law of Conservation of Energy

Any Physics class will discuss the Law of Conservation of Energy which tells us that energy can never be created nor destroyed. In some references, this law is called the Law of Conservation of Work and Energy.
It implies the following:
- It transfers from one object to another.
- It converts from one form to another.
To illustrate, when we exercise, the energy we create from moving turns into heat. We didn't lose said work; it just converted into another form.
Summary
Let's summarize:
Work \(W\) happens if a force or moment causes something to move: \(W=P{\times}{\Delta}\) or \(W=M{\times}{\theta}\). It is a scalar quantity with SI Unit Joule \(J\)
Work only exists if \(F\) and \(\Delta\) or \(M\) and \(\theta\) are acting in the same path.
Work is positive if the net force (or net moment) has the same direction as the displacement (or rotation), while it is negative if the net force (or net moment) and displacement (or rotation) are opposite to each other.
Total work or "net" work is the algebraic sum of all individual work acting on a body.
Virtual work happens when one of these variables, \(F\), \(M\), \(\Delta\), \(\theta\), is an imaginary quantity.
Energy is the ability to do work. It has the SI Unit Joule \(J\)
Energy has two general categories: potential and kinetic energy; The former deals with "energy at rest," while the latter is "energy in motion."
Energy can be expressed in different forms: mechanical energy, electrical energy, and many more.
The Work-Energy Theorem states that the change in kinetic energy equals the total work done on the body.
The Law of Conservation of Energy is an important concept. Energy can never be created nor destroyed.






