A fundamental property in any structure is its ability to resist deflection or deformation. We call this rigidity (or stiffness) \(k\).
Rigidity Types
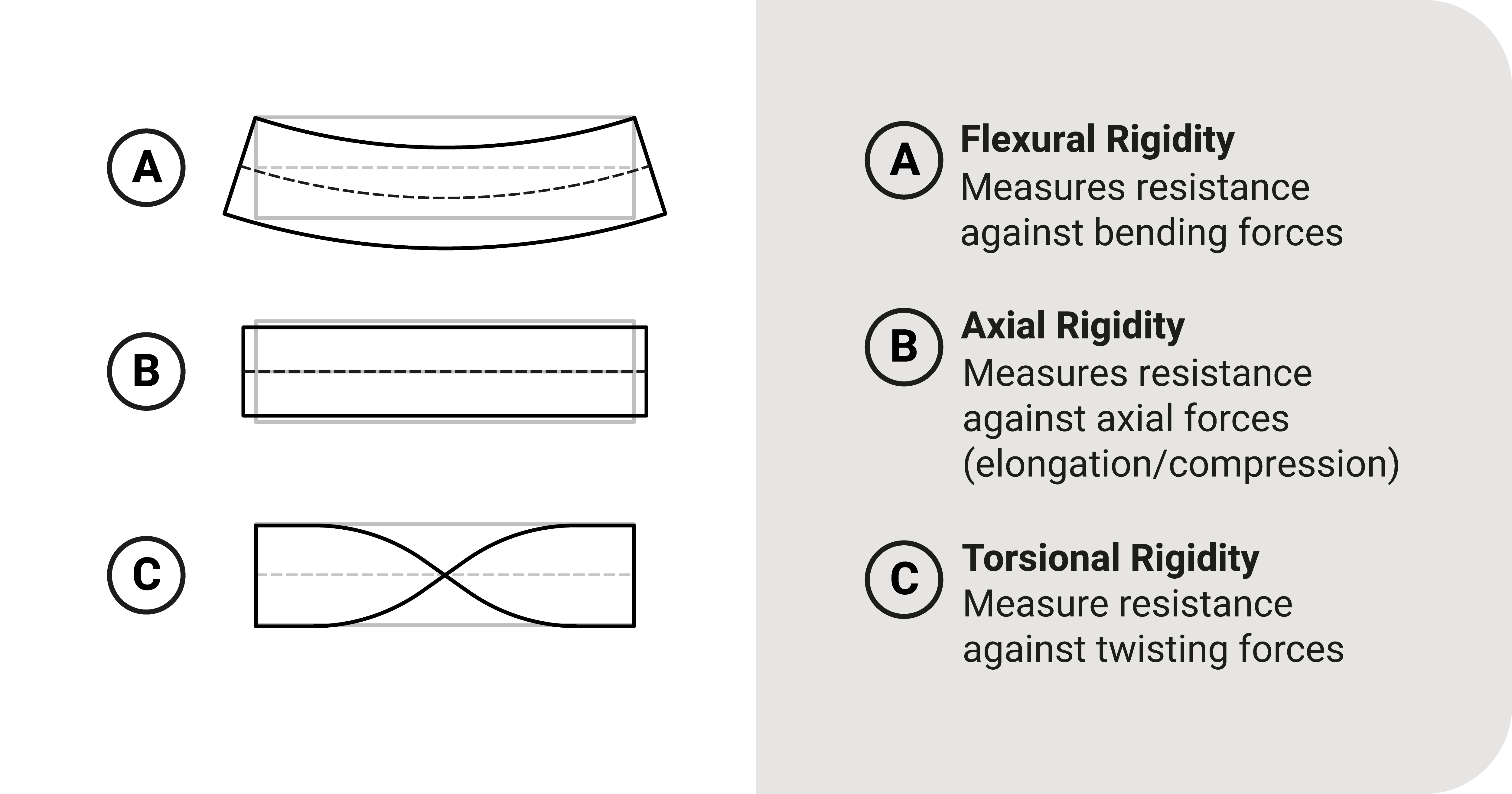
Below are the types of rigidity present in any structure which would depend on the type of internal force:
Flexural
This type measures a structure's resistance to flexural (or bending) loads. It is the product of Young's Modulus \(E\) and the moment of inertia \(I\) of a cross-section.
\(k_f=EI\)
Axial
This type measures a structure's resistance to axial loads. It is the product of Young's Modulus \(E\) and the area \(A\) of a cross-section.
\(k_a=EA\)
Torsional
This type measures a structure's resistance to torsion. It is the product of Shear Modulus \(G\) and the polar moment of inertia \(J\) of a cross-section.
\(k_t=JG\)
Implications
From these different types, we can observe that rigidity is a product of two variables: (1) the inertial properties of the cross-section and (2) the mechanical property of a material.
It implies several things when it comes to the structure's deflection or deformation:
- Rigidity will depend on the cross-section. For example, if we have a tapered beam, the rigidity on its bigger end is more significant than its other end. It means that the smaller end is more prominent to deform or deflect.
- If we want our structure to deform/deflect less, for example, there are two things we can do. First, we may increase its mechanical properties \(E\) or \(G\). It implies that we must find a better material to carry the loads. Second, we may have a larger cross-section. What this does is increase its inertial properties. A bigger \(I\) or \(J\) means the structure will deform less.
Summary
Let's summarize:
A fundamental property in any structure is its ability to resist deflection or deformation. We call this rigidity (or stiffness) \(k\).
There are several types of rigidity: flexural, axial, and torsional. Each rigidity respectively measures resistance with bending, axial, and torsion loads.
Rigidity is a product of two variables: (1) the inertial properties of the cross-section and (2) the mechanical property of a material.



