Whenever we analyze a structure, we may find some forces or deflections we already know from the very start. We call these boundary conditions.
What is the Use of Boundary Conditions?
We might wonder about the use of these conditions. Simply put, it provides us with additional details about the problem.
If we have to make an analogy, it is similar to Differential Equations. We have a general solution to an ordinary differential equation, and you're required to find a particular solution - that only works if you have these so-called boundary conditions.
Example
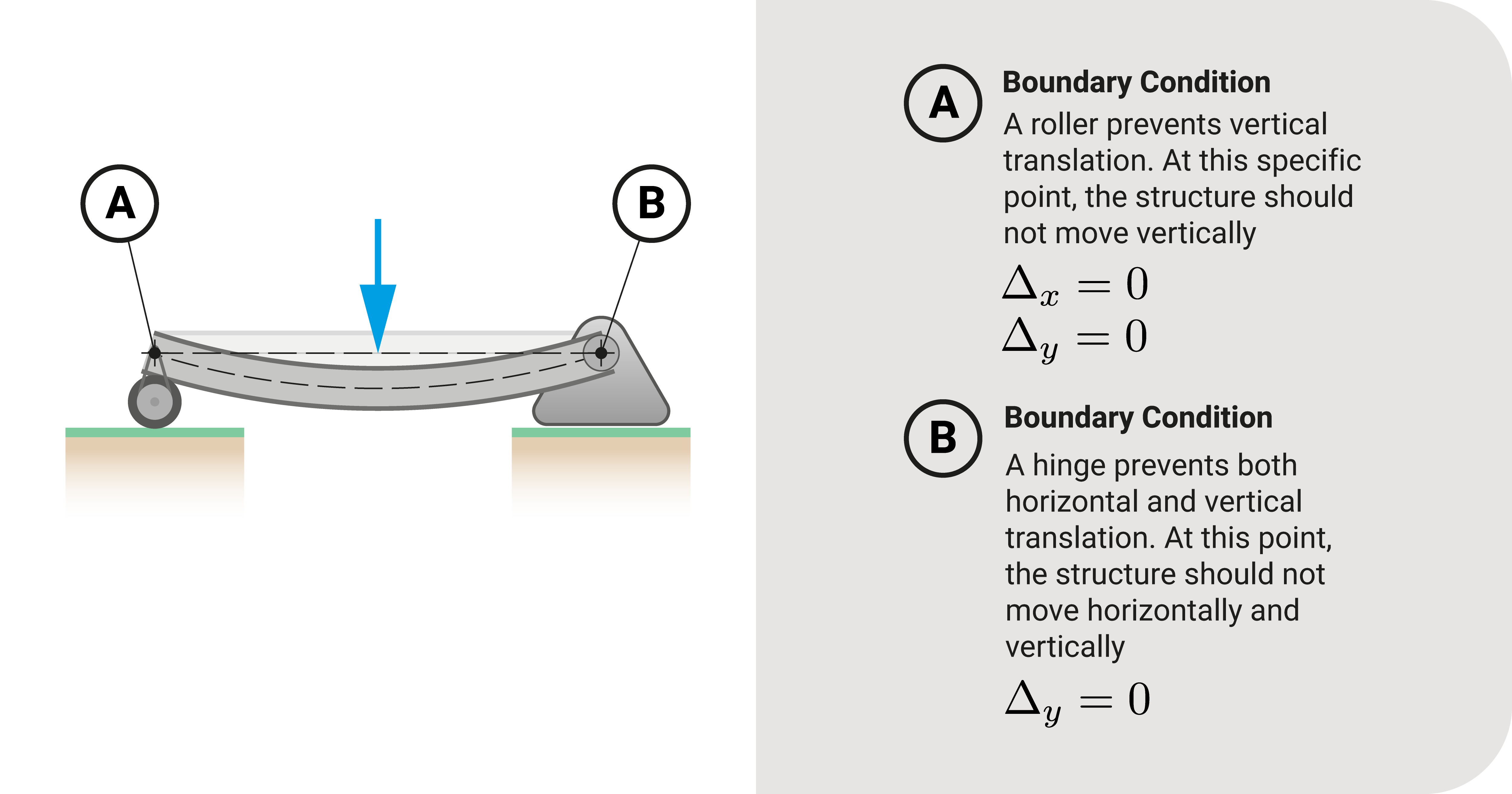
What does a boundary condition look like in a problem? To answer that, let's look at a simple beam.
By inspection alone, we know the following details:
- The vertical translation at the roller support is zero
- Both horizontal and vertical translation at the hinge support must be zero
These two already form the boundary conditions of the problem. From there, we already know the deflection of the beam at those points. It can also aid us as we study this beam more.
Summary
Boundary conditions are forces or deflections at specific points of the structure that we already know from the very start.







