We can analyze structures using work-energy principles in specific structural analysis applications. This post shows how we can apply it. We'll show how we can use the virtual work method to analyze determinate beams.
Key Idea: Virtual Work, Work-Energy Theorem, and Equilibrium
The heart of this method revolves around three concepts: virtual work, work-energy theorem, and static equilibrium. We have a dedicated post if you need a refresher on these topics.
General Outline
The following is a general outline of how to use the virtual work method in beam analysis:
Set Up the Virtual Deflection
We first identify the component we want to solve at a specific point: reaction, shear, or moment. Afterward, we let it do "work" on the beam and allow it to deflect.
For example, say we are to find one of the reactions of a simple beam loaded with a concentrated load \(P\) at the midpoint; we let the unknown reaction force \(R_A\) deflect the beam from its original state to a corresponding deflected shape like the figure shown.
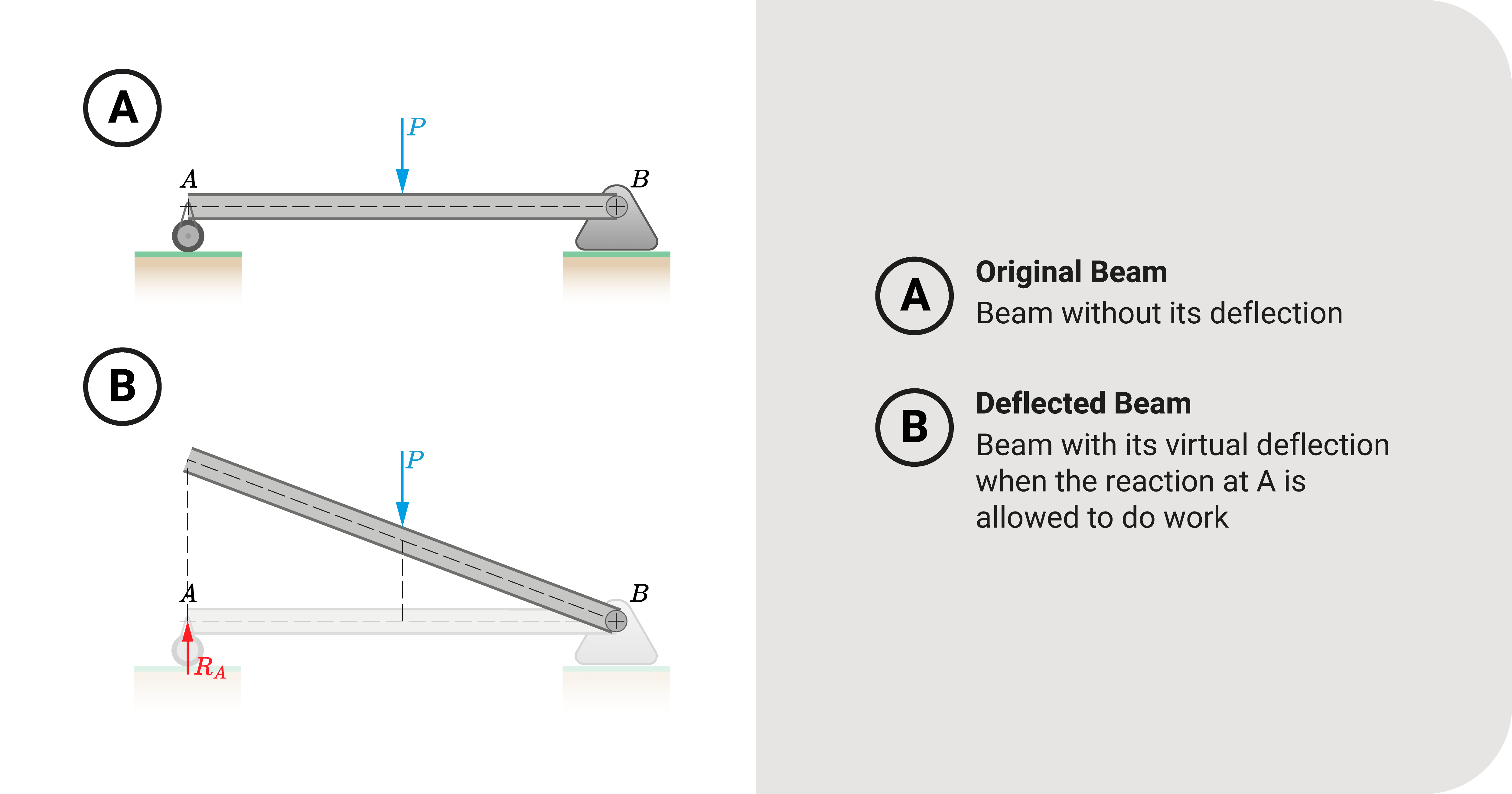
How did we arrive at this deflected shape? Consider the beam as a lever with its reactions as pivot points. When \(R_A\) acts on it, it pushes the beam upward and pivots at the other support.
If we would like to solve for the other components, such as shear and moment, we apply the same concept. Say we would like to find the shear at the midpoint. We first expose it (by cutting a plane section in the middle and splitting the beam into two) and let it do "work" on both parts. Like the example above, the reactions act as pivot points; hence, the left rotates downward about the left-side support while the right rotates upward about the right-side support.
The deflected shape serves as our set-up when using the virtual work method. One important thing to note is that this shape is fictional. All translations and rotations resulting from letting the components do "work" on the beam are imaginary.
The purpose of this is to provide the fictional \(\Delta\) or \(\theta\) we need later on and create relationships from them.







