Let's illustrate how to find shear and moment using the equations. Below are sample expressions taken from this example:
Shear Equations
\(V_{AB}=0,\{0\leq{x}\lt {2}\}\)
\(V_{BC}=-5x^2+20x+70,\{2\leq{x}\lt {6.5}\}\)
\(V_{CD}=-36x+222.75\{6.5\leq{x}\lt {11}\}\)
\(V_{DE}=90,\{11\leq{x}\lt {12.5}\}\)
Moment Equations
\(M_{AB}=27,\{0\leq{x}\lt {2}\}\)
\(M_{BC}=-\frac{5}{3} x^3+10 x^2+70 x-139 \frac{2}{3},\{2\leq{x}\lt {6.5}\}\)
\(M_{CD}=-18 x^2+222.75 x-407.25\{6.5\leq{x}\lt {11}\}\)
\(M_{DE}=90x-1125,\{11\leq{x}\lt {12.5}\}\)
Evaluating Shear and Moment
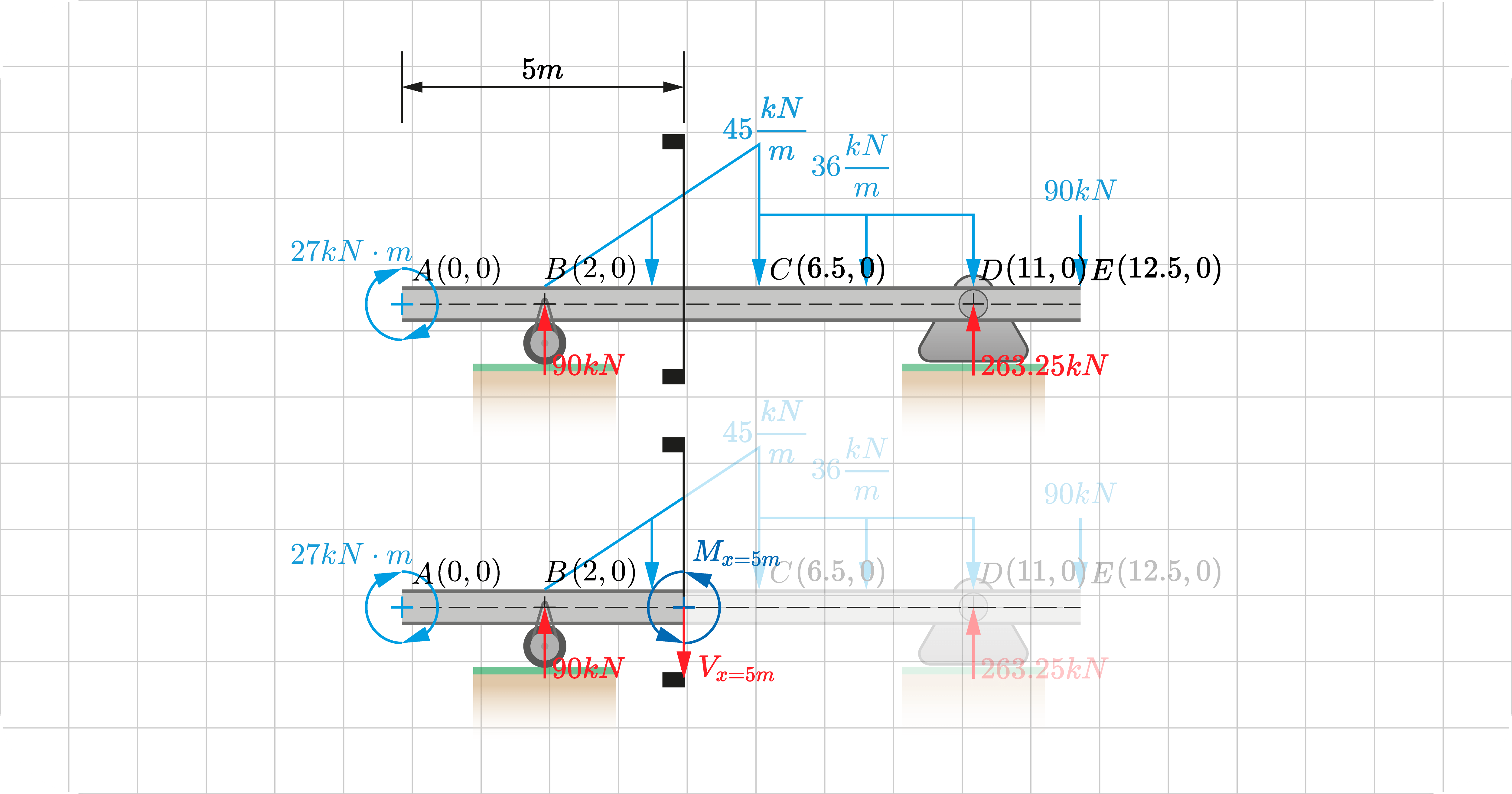
Say we're interested in finding the shear and moment at \(x = 5m\). We first determine the appropriate shear and moment equation to use. Since \(x=5\) is between points \(B\) and \(C\), we use these equations:
\(V_{BC}=-5x^2+20x+70,\{2\leq{x}\lt {6.5}\}\)
\(M_{BC}=-\frac{5}{3} x^3+10 x^2+70 x-139 \frac{2}{3},\{2\leq{x}\lt {6.5}\}\)
Using these, we substitute and evaluate the following:
\(V_{x=5}=-5x^2+20x+70,\{2\leq{x}\lt {6.5}\}\)
\(V_{x=5}=-5(5)^2+20(5)+70\)
\(V_{x=5}=45kN\)
\(M_{x=5}=-\frac{5}{3} x^3+10 x^2+70 x-139 \frac{2}{3},\{2\leq{x}\lt {6.5}\}\)
\(M_{x=5}=-\frac{5}{3} (5)^3+10 (5)^2+70 (5)-139 \frac{2}{3}\)
\(M_{x=5}=252kN\bullet{m}\)
Shear and Moment Diagrams
We can graphically express the shear and moment of a structure.
The following shows the graphical representation of these components.







