Pressure varies depending on the depth. Because of this, the fluid force acting on the object differs depending on the depth; hence, the computation for the total force will require integration.
WeTheStudy lets you connect ideas
Learn more

In this post, we'll explore how to find the total force acting on an object in a fluid experiencing varying forces.

Varying Fluid Force

Let's say we have a submerged plate oriented vertically in a fluid with uniform unit weight. In addition, let's also consider its pressure solid. From this graph, pressure increases from the top of the object to its bottom. It implies that pressure varies depending on the depth.

To find the total force \(F\) acting on the body, it is \(F=\gamma h A\); however, because pressure varies, the fluid force on the bottom of the plate is not the same as that of the top.

Approximation

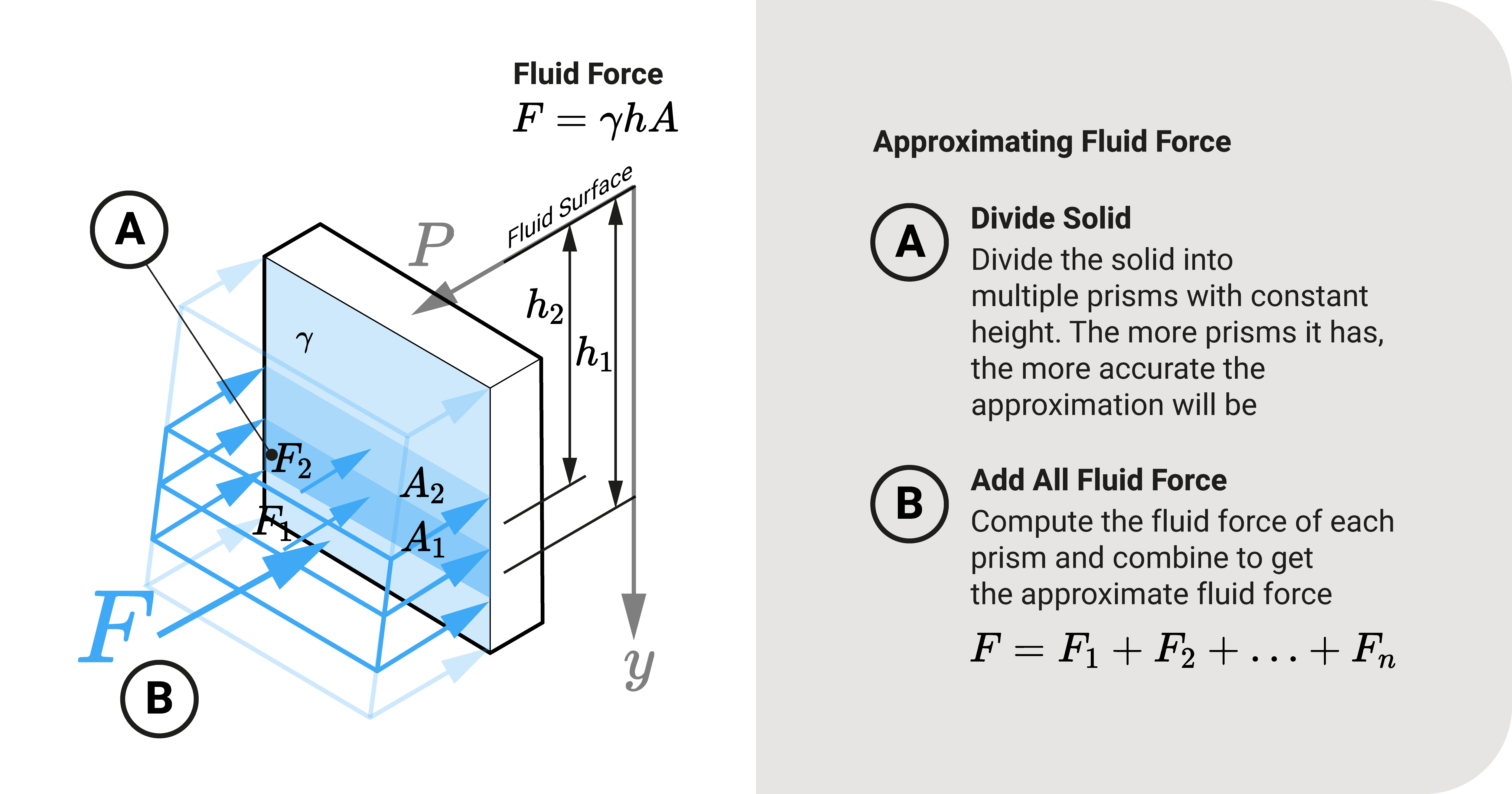
Approximating the fluid force exerted on an object

To compute the total force, we can approximate it. We divide the pressure solid into multiple solid sections. This would result to submerged cross-sectional areas \(A_1\), \(A_2\), \(A_n\). From this, we establish the heights \(h_1\), \(h_2\), \(h_n\) of these areas from a reference. We can compute the fluid force for each division as follows:

\(F_n = \gamma h_n A_n\)

The total force is then the sum of these individual fluid forces. If we want a better approximation, we increase the number of solid sections.

Want to access the remaining content?
You're a Member!
Click to expand on exclusive content
Want to access the remaining content?

Become a Member

When you sign-up and subscribe to WeTheStudy, you’ll get the following benefits:

No ads! (yey!)
Complete access to all articles
Ability to track your progress in the tree

SIGN-UP

Complete Your Checkout

When you complete your account, here are the following benefits:

No ads! (yey!)
Complete access to all articles
Ability to track your progress in the tree

PROCEED CHECKOUT

Exact Solution

Finding the exact fluid force acting on an object

Borrowing this idea from approximation, we can determine the pressure solid's total fluid force using integration. If we consider multiple differential fluid force \(dF\) and sum all of these, we have the total fluid force \(F\) as:

\(F = \int dF\)

  • \(F\) is the total fluid force
  • \(dF\) is the differential fluid force
The differential fluid force

Let's expand on \(dF\), it is equal to:

\(dF = \gamma h dA\)

As a result, \(F\) is equal to:

\(F = \int_{a}^{b} \gamma h dA\)

  • \(F\) is the total fluid force
  • \(a\) is the lower limit (origin - fluid surface)
  • \(b\) is the upper limit (total depth of surface)
  • \(\gamma\) is the unit weight of the fluid; If the unit weight varies per height, it must be a math function of \(y\)
  • \(h\) is the height from the fluid surface. Usually, a math function of \(y\)
  • \(dA\) is the differential area.

The differential area \(dA\) will depend on the surface we want to investigate. Generally, it is equal to:

\(dA = L dy\)

  • \(dA\) is the differential area of the submerged surface
  • \(L\) is the length of the surface. Must be a function of \(y\)
  • \(dy\) is the height dependent variable

These equations are the general formula for the total fluid force acting on the submerged project. It is the equation we use to solve for the fluid force of any pressure solid.

Summary

It implies that pressure varies depending on the depth. Because of this, the fluid force acting on the object differs depending on the depth.
The general expression for finding such an object is \(F = \int_{a}^{b} \gamma h dA\). \(F\) is the total fluid force, \(a\) is the lower limit (origin - fluid surface), \(b\) is the upper limit (total depth of surface), \(\gamma\) is the unit weight of the fluid; If the unit weight varies per height, it must be a math function of \(y\), \(h\) is the height from the fluid surface - usually, a math function of \(y\), and \(dA\) is the differential area.
The differential area is \(dA = L dy\). \(dA\) is the differential area of the submerged surface, \(L\) is the length of the surface - it must be a function of \(y\), and \(dy\) is the height dependent variable

No ads?

Tree Navigation

See how this article relates to other ideas
Children
No children (yet)
Siblings
No siblings (yet)
Parent

#

1

What is Fluid Force?

A body submerged in a fluid will experience fluid pressure. The equivalent resultant force of such pressure is what we call the fluid force. Let's explore this concept.

Connections

#

1

How to Solve Volume Using Integration?

We can determine the volume of a solid with similar cross-sections using definite integrals. In this post, let's explore how it expands the approximate solution.

Created On
June 5, 2023
Updated On
February 23, 2024
Contributors
Edgar Christian Dirige
Founder
References

WeTheStudy original content

Revision
1.00
Got some questions? Something wrong? Contact us
This account is currently deactivated due to a
failed payment. Update your payment method now