An object in a fluid will experience fluid force. Let's explore more on this event:
Fluid Force
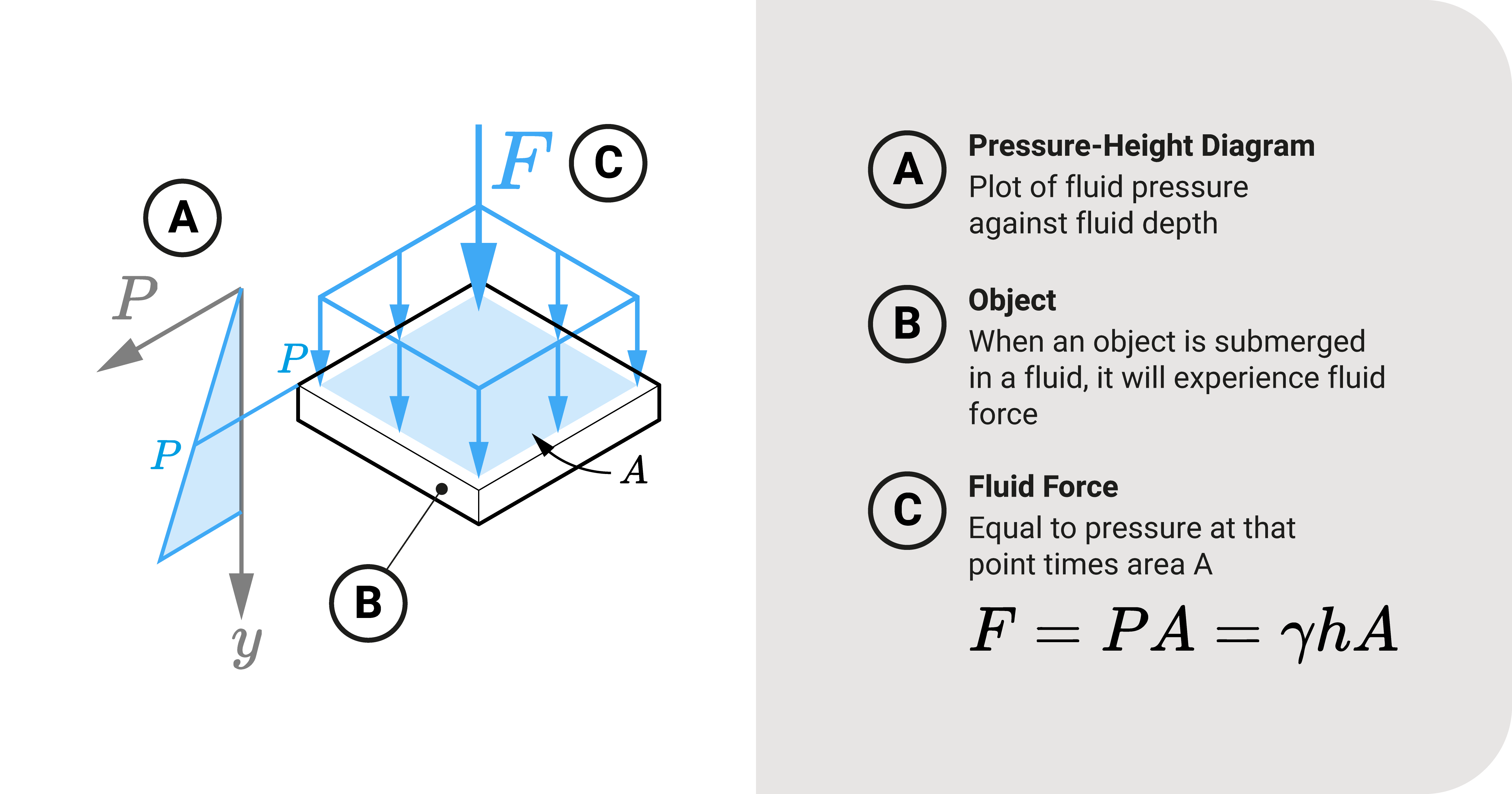
To derive an equation for computing the fluid force \(F\) experienced by a submerged object with cross-section \(A\), remember that pressure is:
\(P=\frac{F}{A}\).
\(F=PA\)
Since fluid pressure is \(P=\gamma h\), we can express fluid force on an object as:
\(F=\gamma h A\)
- \(F\) is the fluid force acting on the object
- \(\gamma\) is the unit weight of the fluid
- \(h\) is the height (or depth) of the fluid from a reference
- \(A\) is the submerged cross-section area at height/depth \(h\)
Constant Versus Varying Force
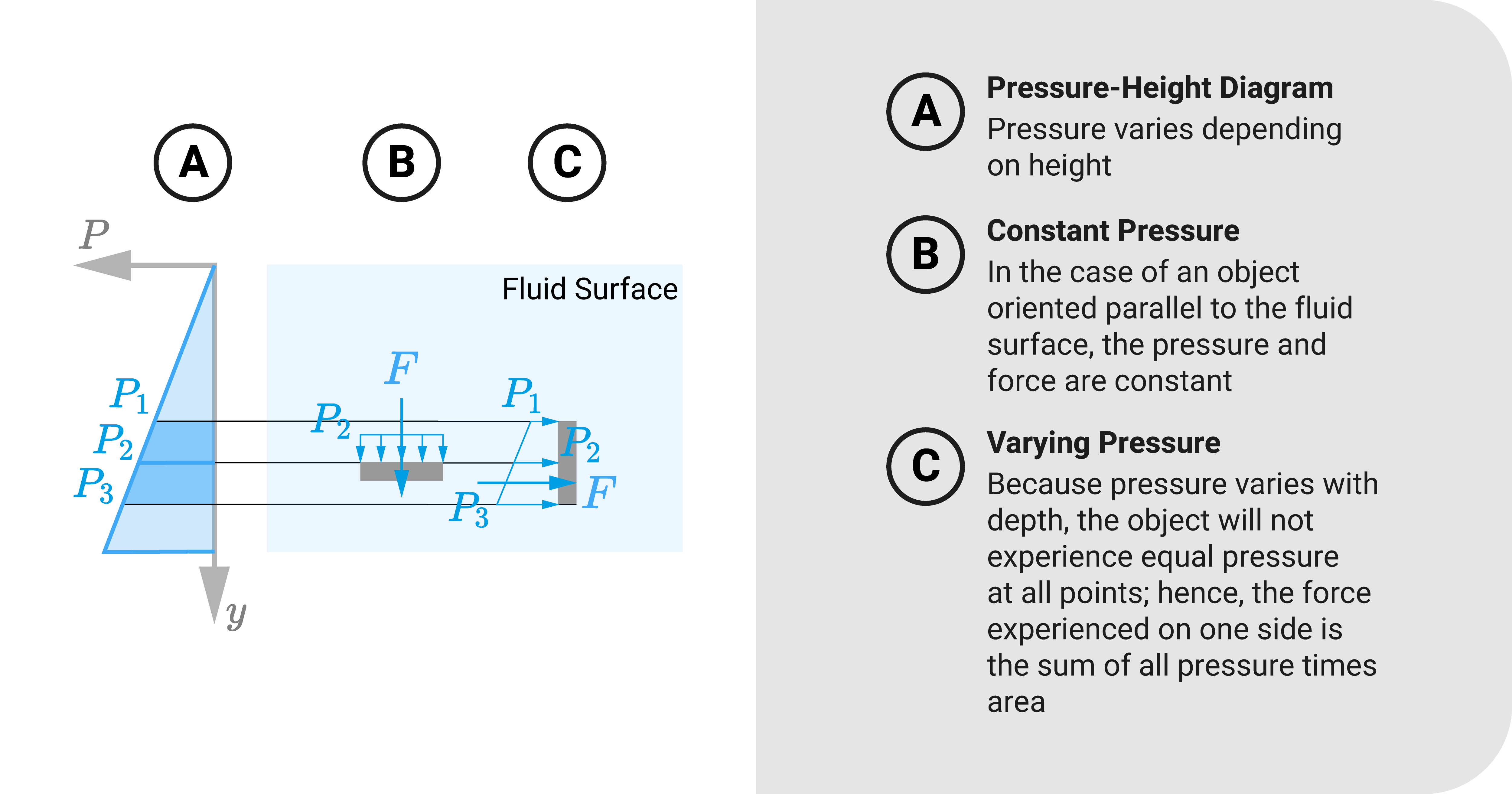
Let's recall an essential expression in fluid statics: an object going deeper into a fluid will experience more pressure: \(P=\gamma h\).
As such, an object submerged in a fluid may experience constant or variable fluid force. To illustrate, consider the two plates.
- We have a plate in a horizontal position (parallel to the surface)
- The other plate is in a vertical position (perpendicular surface)
In the former, the horizontal plate experiences constant pressure because it's on the same level. The fluid force is equal to \(F=\gamma h A\); however, for the vertical plate, the top experiences lesser pressure than the bottom. As a result, the fluid force varies.
Pressure Solids
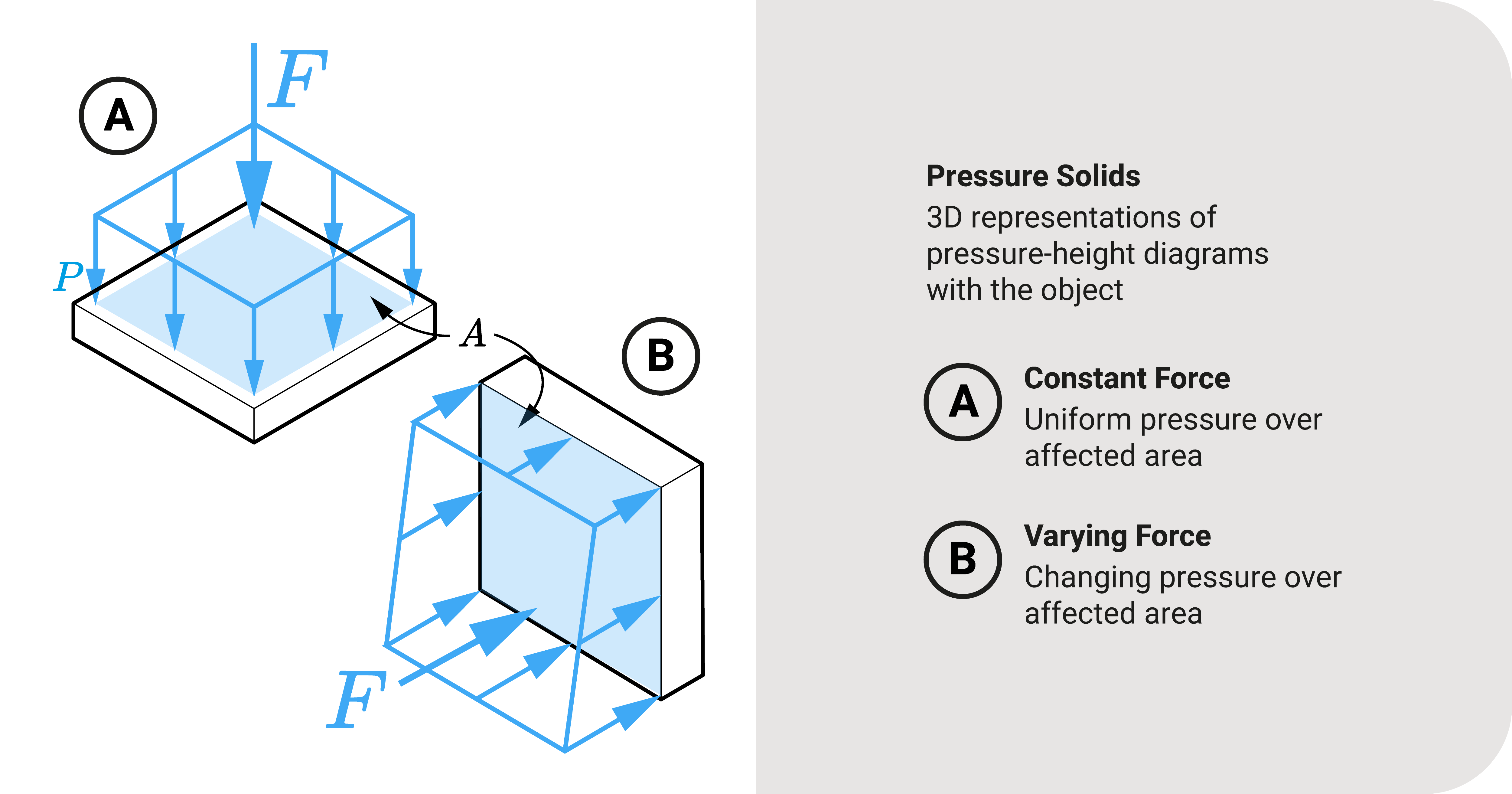
We can expand the pressure-height diagram into 3D if an object is in the fluid. We call this the pressure solid.
We can determine the total force acting on the object from the pressure solid.
If the pressure solid has a uniform cross-section area throughout its length, sometimes, we refer to it as the pressure prism.
Summary
The fluid force experienced by an object submerged in a fluid is equal to the product of unit weight \(\gamma\), height from a reference \(h\), and cross-sectional area of the body \(A\) at height \(h\): \(F=\gamma h A\)
An object going deeper into a fluid will experience more pressure. As such, an object submerged in a fluid may experience constant or variable fluid force depending on its orientation.
If we orient an object on the same level in a fluid, it will experience constant pressure; If we orient it otherwise, the object experiences varying pressure: lesser at its top than at its bottom. We can see how the force acts in these two situations using a pressure-height diagram.
We can expand the pressure-height diagram into 3D if an object is in the fluid. We call this the pressure solid.
We can determine the total force acting on the object from the pressure solid.






