Finding the volume of a solid by integration is another critical integration application. This post explains the theory behind it. At the end of this post, we'll be able to find the volume of an object with a constant cross-section, no matter how complicated it may be.
Approximation
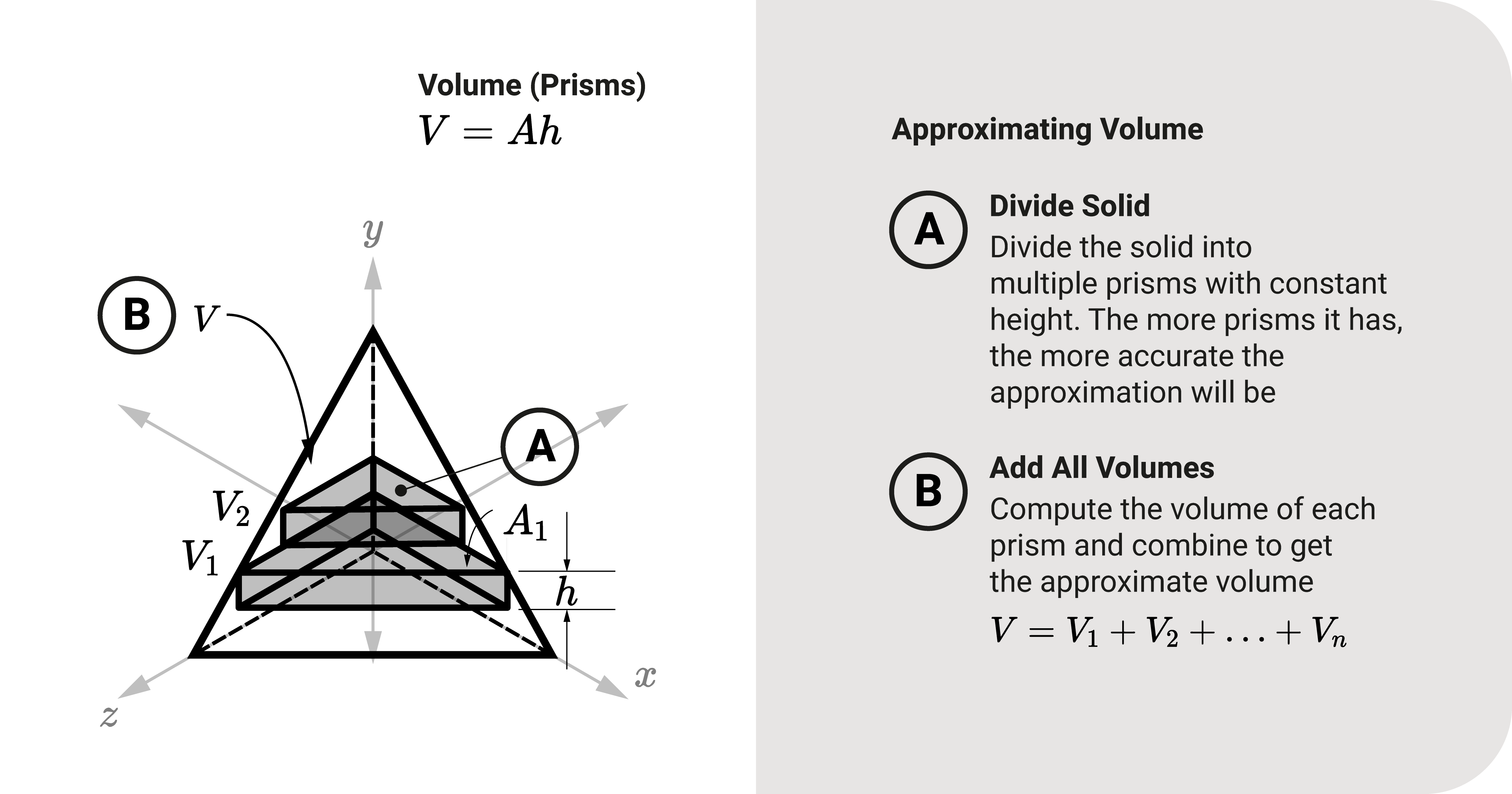
Let's say you're finding the volume \(V\) of the solid figure shown. The object consists of a uniform cross-section throughout its whole length. We can find \(V\) using solid geometry if it is an elementary geometric figure. For unusual solids, the best we can do is approximate them.
We must divide the solid into multiple parts to estimate the total volume. To do that, imagine the solid as a series of plane sections stacked on each other.
A similar illustration would be a paper ream. That one rectangular ream object consists of multiple sheets of paper. That is how we view the solid - layers making up the 3D object.
Another critical thing to note is that the plane sections that make up the solid must be similar. In our ream example, the cross sections must be rectangular only.
From this, we begin the process of approximating by:
- First, divide the 3D object into multiple regular solids. It could be cubes, prisms, cylinders, or any other figure.
- Then, we solve the volume \(V\) of each divided solid. From Cavalieri's theorem, \(V=Ah\) where \(A\) is the uniform cross-sectional area and \(h\) is the length of the solid
- Finally, we add all individual \(V\) to get the total approximate volume.
Since this is an approximation, how can we have a more accurate answer? We increase the number of divisions \(n\).
- When we increase the number of solid divisions, the more closely it would lead to the actual value.
- As the number of solids increases, the smaller its volume \(dV\) and height \(h\) become.








