Deflection, at its basic dictionary definition, is an act of moving out from its course. In structural analysis, this has a similar concept.
Deflection, Neutral Shape, and Deflected Shape
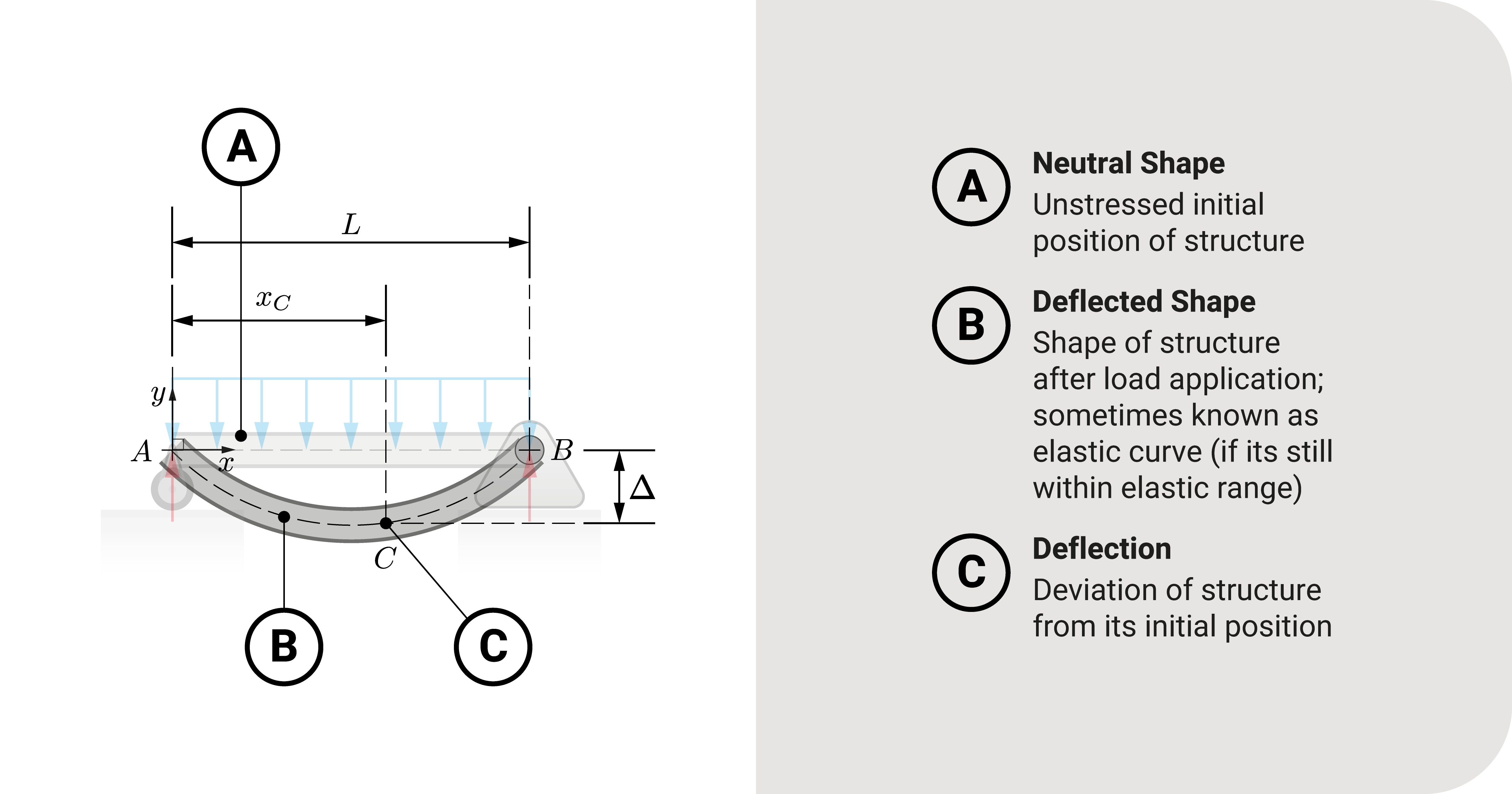
Every object/structure has an initial position called the neutral shape - the structure's shape when no loads are applied. When it experiences loads, every structural point will deform (change shape) and deflect (move) from its original position. The resulting shape is what we call its deflected shape.
The measure of how much a point moved from its original place is what we call deflection. Part of any structural analysis is to investigate this behavior.
Naturally, when a structure deflects, it will try to resist it. This property is what we call rigidity. Later on, we will see how it fits with the topic.
Types of Deflection
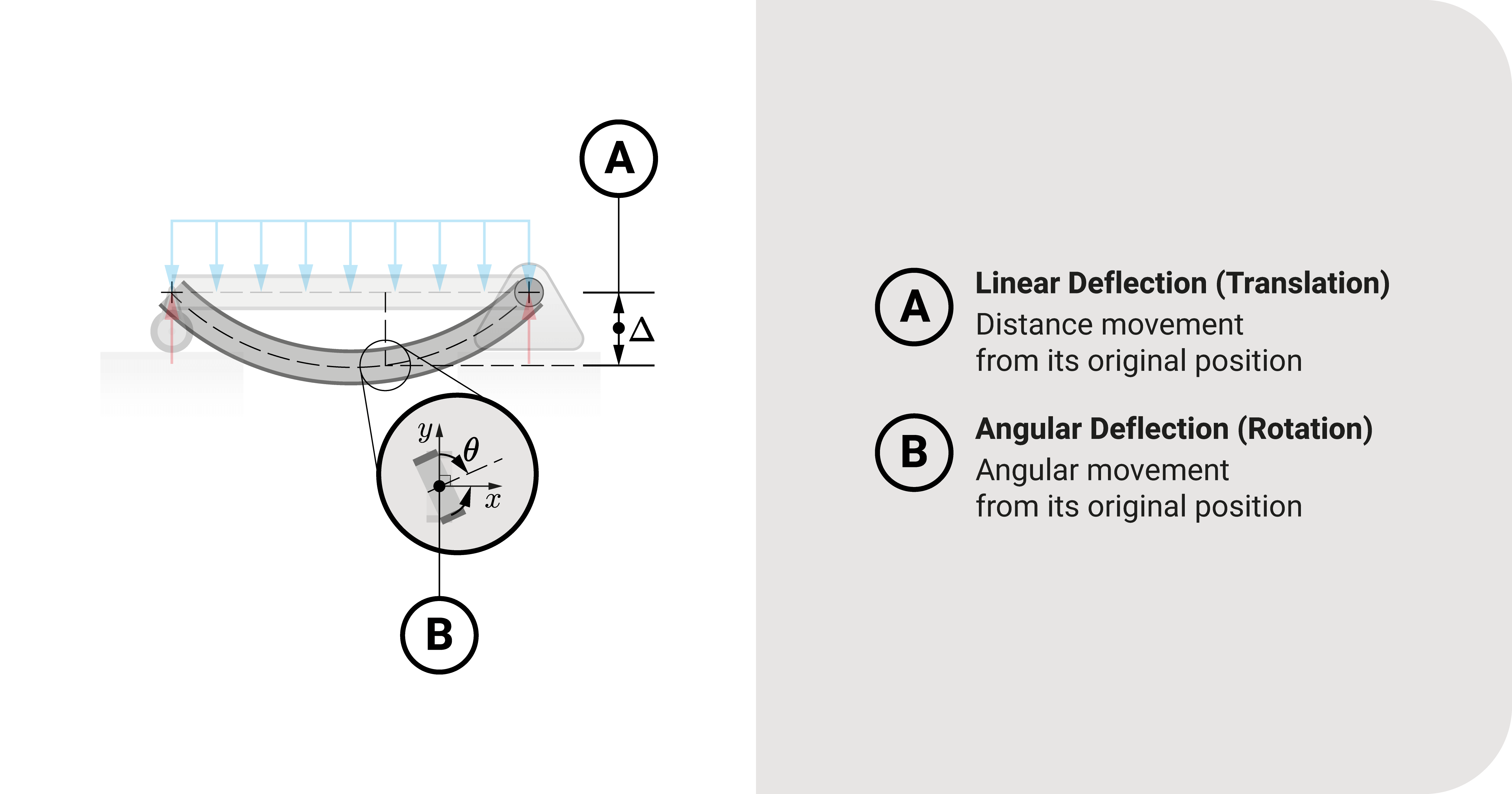
Let's move on to deflection types. There are two types of deflection: linear (translation) and angular (rotation).
The first type, translation, measures how much a point in the structure has moved from its original position. It may translate a few millimeters from its neutral position.
On the other hand, the second type, rotation, measures how much a point in the structure has rotated from its original position. It may rotate by a few degrees from its initial position.
Notation
For this reference, we will use the following convention when naming deflections:
Real Load Notation
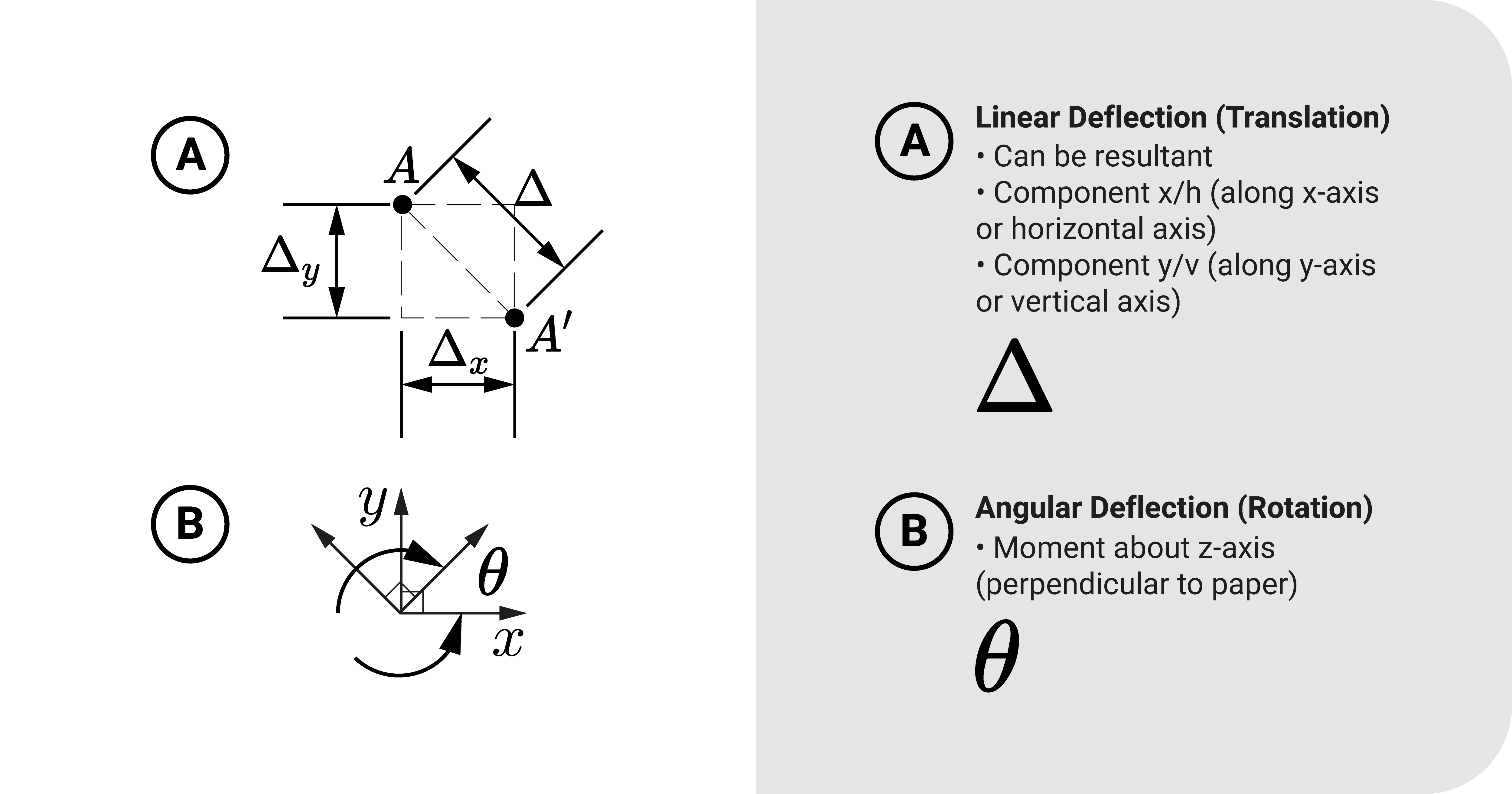
If a structure experiences actual loads, the notation for deflections is the following:
- Linear translation \(\Delta\). For horizontal components, it is either \(\Delta_h\) or \(\Delta_x\). On the other hand, for vertical components, it is either \(\Delta_v\) or \(\Delta_y\)
- Angular translation / Rotation \(\theta\)
The translation is the uppercase Greek letter delta \(\Delta\), while rotation is the Greek letter theta \(\theta\).
Components
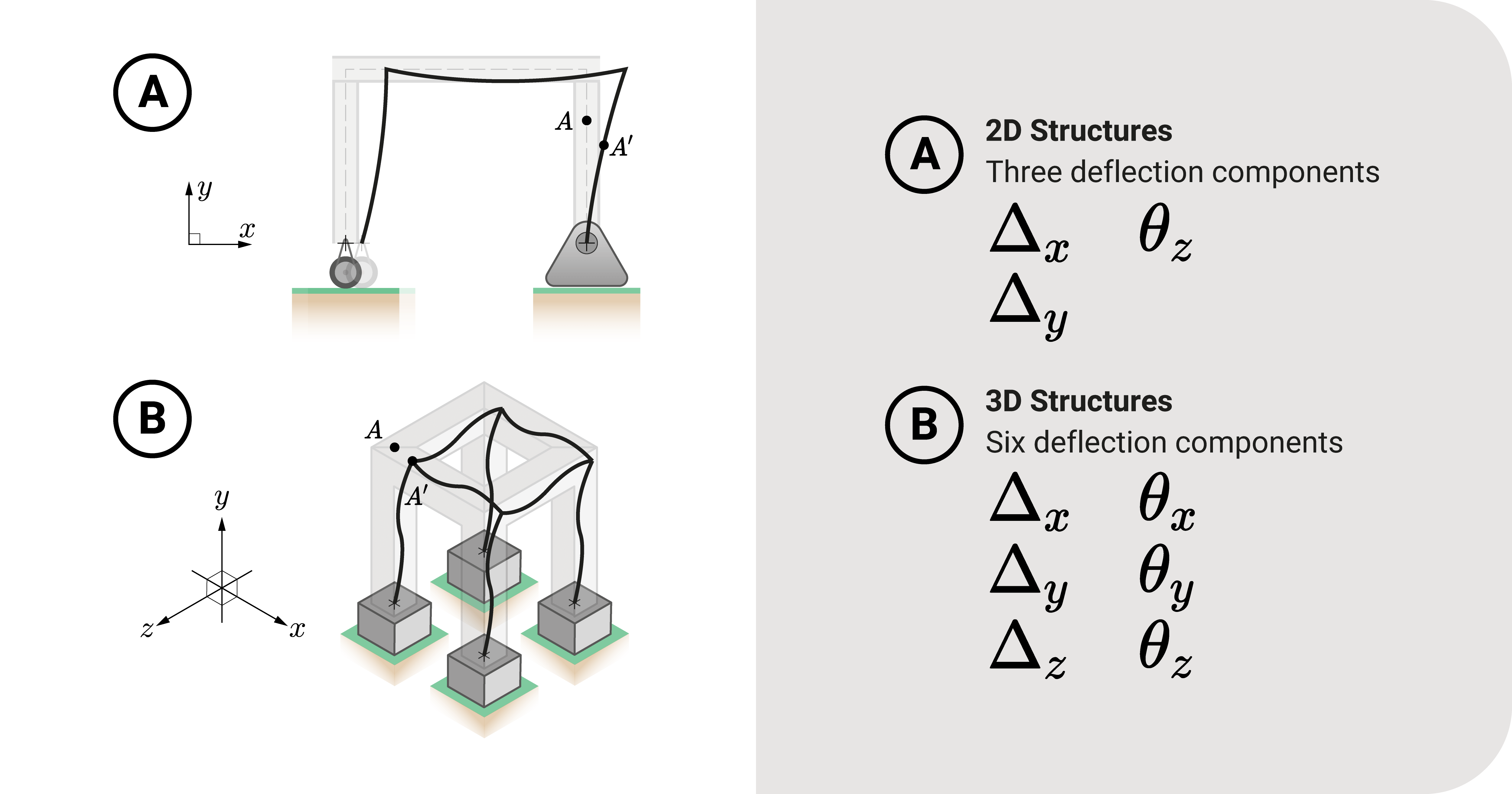
Let's consider a structure with a pre-defined grid. A point in the structure may translate along the \(x\), \(y\), and \(z\)-axes. Likewise, it may rotate about the \(x\), \(y\), and \(z\)-axes.
We may represent these deflections as a single result, but it's usually best to break them down into their components.
- When we are considering a 3D structure, there would be six deflection components: translation in the \(x\), \(y\), and \(z\) and the rotations about the \(x\), \(y\), and \(z\).
- For 2D structures, there are only three deflection components: translation in the \(x\), \(y\), and the rotation about the \(z\).
Summary
Let's summarize:
Every object/structure has an initial position called the neutral shape - the structure's shape when no loads are applied.
When it experiences loads, every structural point will deform (change shape) and deflect (move) from its original position. The resulting shape is its deflected shape.
The measure of how much a point moved from its original place is what we call deflection.
There are two types of deflection: linear (translation) and angular (rotation)
The first type, translation, measures how much a point in the structure has moved from its original position.
The second type, rotation, measures how much a point in the structure has rotated from its original position.
We may represent these deflections as a single result, but it's usually best to break them down into their components.
When we are considering a 3D structure, there would be six deflection components: translation in the \(x\), \(y\), and \(z\) and the rotations about the \(x\), \(y\), and \(z\).
For 2D structures, there are only three deflection components: translation in the \(x\), \(y\), and the rotation about the \(z\).








