Let's recall that a structure comprises of different components, such as supports, joints, and members. When modeling these, we must consider the positioning of these parts. We want it to have the proper arrangement. A building may suddenly collapse if we have poorly positioned these parts.
To guarantee a good arrangement, we first analyze the structure's stability before making any analysis. When we refer to stability, it is the ability to retain rigidity and shape when applied with loads.
When do we say a structure is stable? It is such if it is both externally and internally stable. Let's discuss each type:
External Stability
This type deals with stability concerning the structure's supports. Let's consider that the model is a rigid body. To say it is externally stable, it must satisfy two things:
Proper Arrangement of Supports
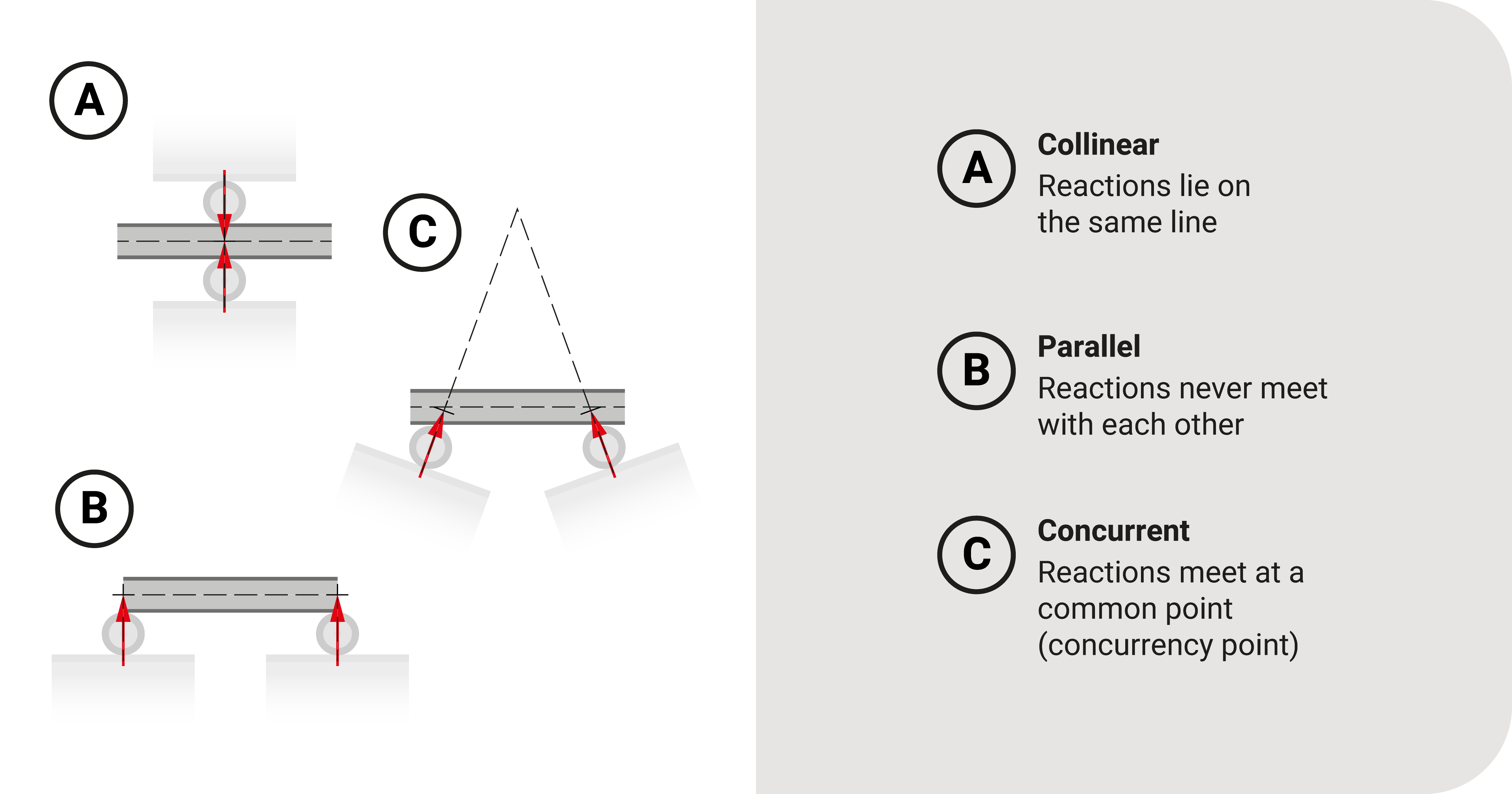
The first rule is to check if the supports are in the correct position. Specifically, the action line must not be:
- Collinear. Lines lie on the same line.
- Parallel. Lines will never meet with each other.
- Concurrent. Lines meet at a common point (known as the concurrency point).
These situations make the structure unstable because they cannot support specific load arrangements. For instance,
- When all support components lie on the same line, they cannot resist forces on a line perpendicular to the supports.
- When all support components are parallel, they cannot prevent the body from sliding.
- When all support components meet at a common point, they cannot resist any moment about the said point.
Unstable Equilibrium
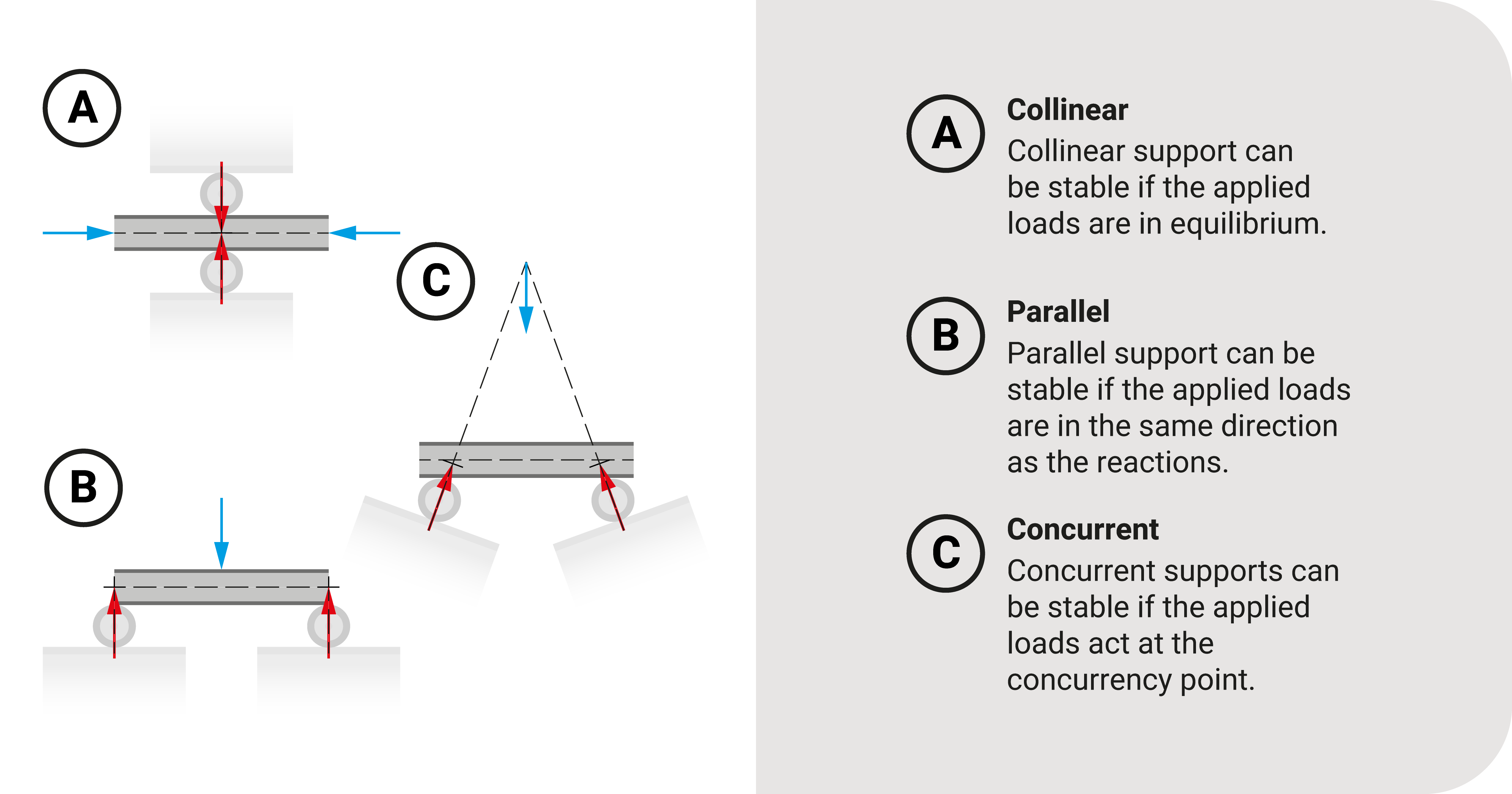
There are unique instances when the structure can be stable even if the supports are collinear, parallel, or concurrent; however, these instances would require specific load arrangements:
- Collinear support can be stable if the applied loads are in equilibrium. In this arrangement, the reactions are optional.
- Parallel support can be stable if the applied loads are in the same direction as the reactions. In other words, the loads and supports form a parallel force system.
- Concurrent supports can be stable if the applied loads act at the concurrency point. When this happens, no overturning can happen at that point.
Even if these special situations would stabilize a structure, these are still unstable. Civil buildings must be durable for any loads they may experience.
Number of Supports ≥ Number of Equilibrium Equations
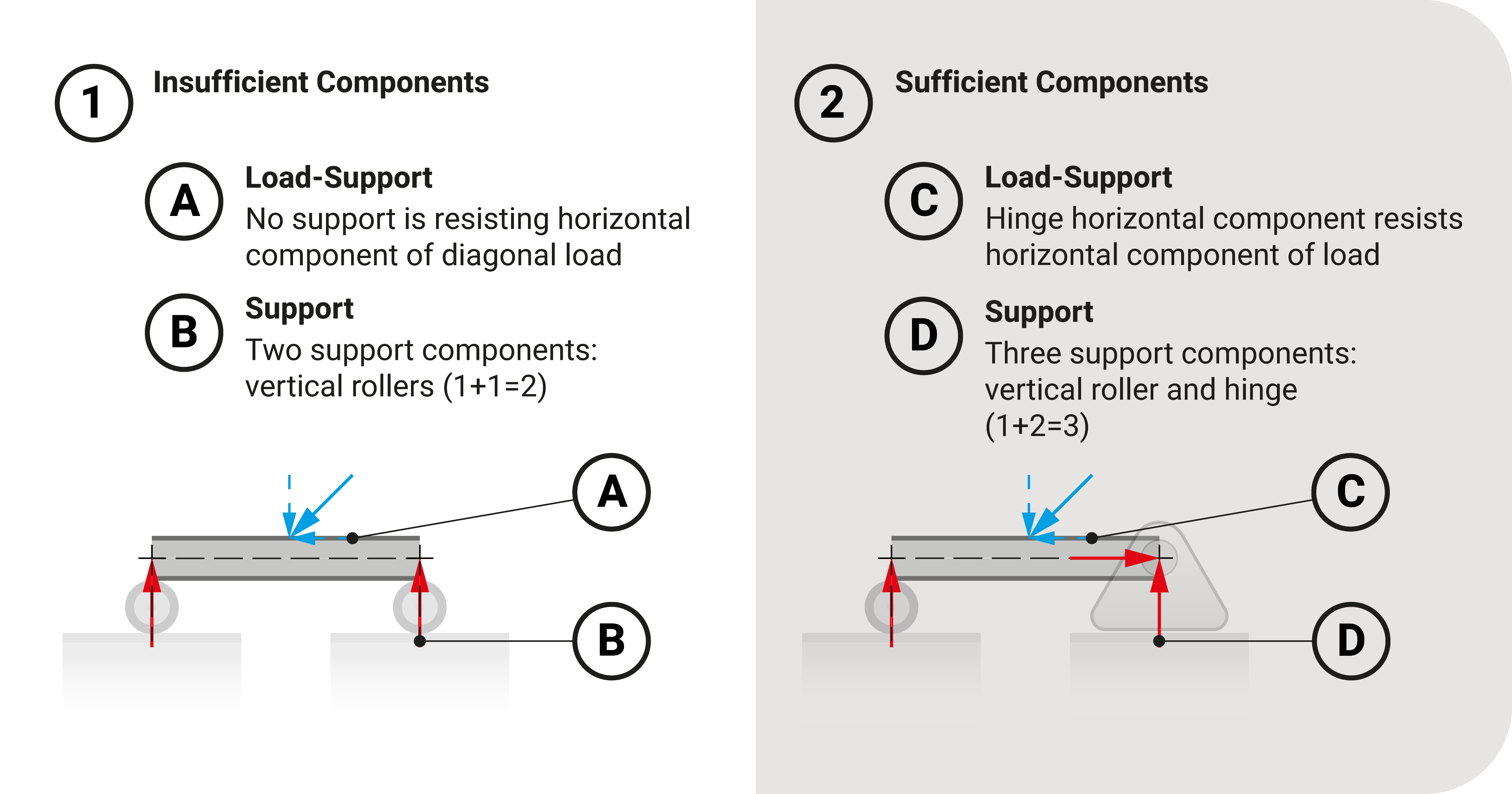
The second criterion is to check if the number of reaction components equals or exceeds the number of equilibrium equations.
What happens if it is less than the number of equilibrium equations? Generally, we will be breaking such a key concept. Imagine two rollers supporting a 2D beam loaded with a diagonal load. If we use \({\sum}F_{x}=0\) to evaluate it, we will NOT satisfy the equation because no support is resisting the horizontal component of the diagonal load.
We'll need something to resist such load to make it stable. Say we change one of the rollers to a hinge. In this instance, the hinge will help withstand the load.
We can have more than the required number of supports. Additional supports will provide more resistance and stabilize the building (provided that there is proper arrangement of supports).
Internal Stability
This type deals with a structure's stability concerning its arrangement and connections. Generally, this instability occurs when we have the following:
- Wrong location of internal connections, such as hinges or links,
- Wrong placement of members
These conditions will depend on the type of structure which we will explore soon.
Summary
Stability is the structure's ability to retain rigidity and shape when applied with loads.
There are two types of stability: external and internal.
External stability deals with a structure's stability concerning its supports, while internal stability deals with a structure's stability concerning its arrangement and connections.
Two criteria must be satisfied to achieve external stability of a rigid-body structure. First, there must be a proper arrangement of supports - they should not be collinear, parallel, or concurrent, and (2) the number of reaction components must be equal to or greater than the number of equilibrium equations.
Analysis for internal stability will depend on the arrangement of the components.






