Another helpful procedure for determining deflection components at specific points is the area moment method (or moment area method). We use this to find rotation and translation for 2D beams and frames.
Unlike the double integration method, which is purely analytical, this solution requires you to analyze its deflected shape geometrically.
Key Idea: Area-Moment Theorems
Two fundamental theorems lay the foundation of this method: (1) change in slope and (2) tangential deviation—both of these theorems came from the Bernoulli-Euler Beam Model.
Theorem 1: Change in Slope
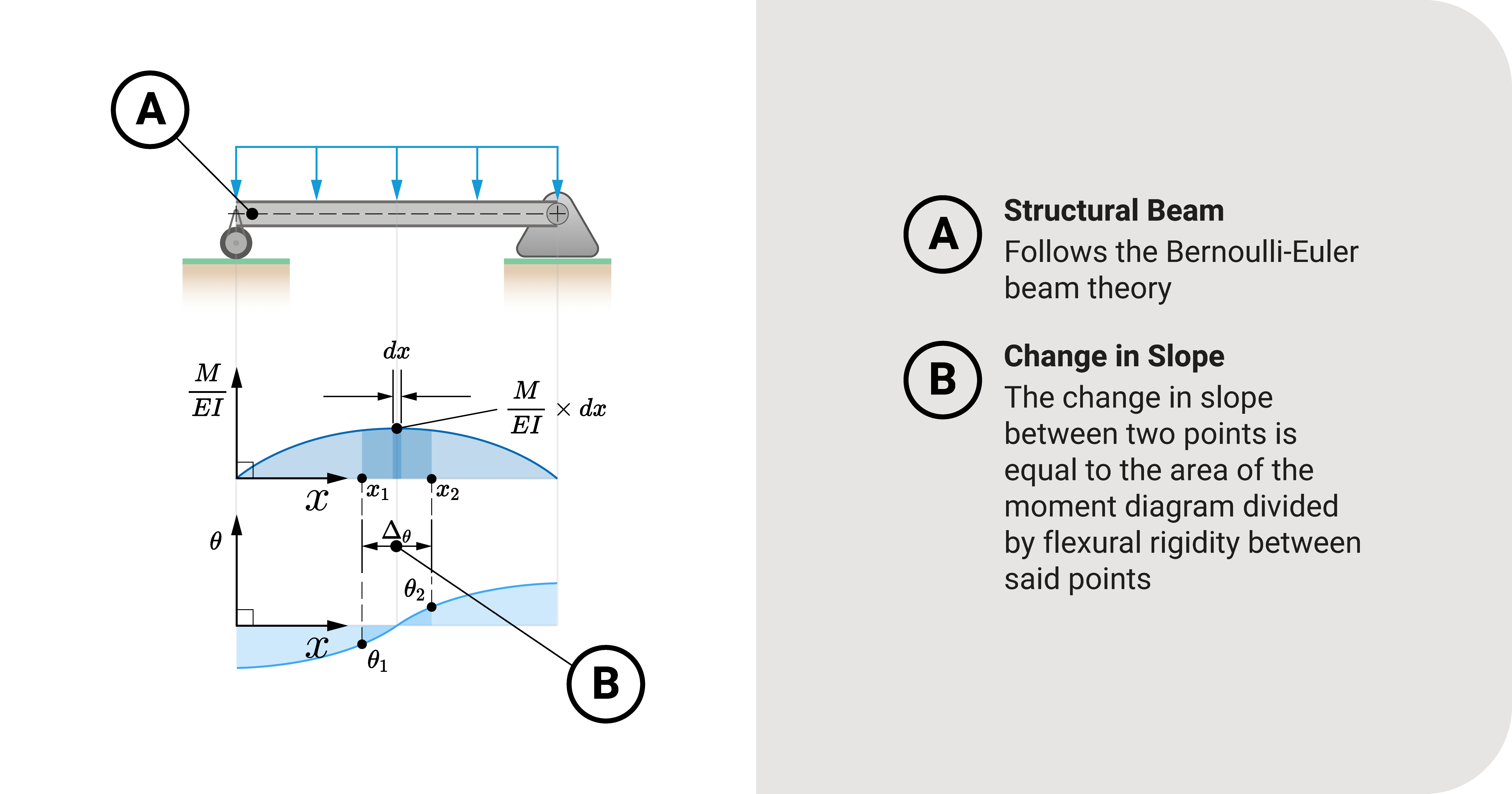
The first theorem revolves around finding the difference between rotations between two points:
\(\Delta_\theta=\theta_2-\theta_1=\int_{x_1}^{x_2}\frac{M}{EI}dx\)
"The change in slope between two points \(x_1\) and \(x_2\) is equal to the area of the \(\frac{M}{EI}\) diagram between said points."
Theorem 2: Tangential Deviation

The second theorem revolves around finding the deviation of a point from a reference:
\(t_{x_2/x_1}=\int_{x_1}^{x_2}\frac{M}{EI}\bar{x}dx\)
"The tangential deviation of point \(x_2\) from \(x_1\) is equal to the first moment of the area of the \(\frac{M}{EI}\) diagram."
Using the Area Moment Method
Let's move on to how to apply the area moment method. Generally, you can approach the problem in two ways:
It is best to illustrate these through examples.
Summary
Let's summarise:
The area moment method is an analytical and geometric procedure used to find the deflection of plane beams and frames.
Two fundamental theorems lay the foundation of this method: (1) change in slope and (2) tangential deviation.
Generally, you can approach the problem in two ways: Integration or Moment By Parts.











