Continuing from free fall motion with air resistance, we know that we can describe such movement using these relations:
\(v(t)=\sqrt{\frac{m g}{k}} \tanh \left(\operatorname{arctanh}\left(v_0 \sqrt{\frac{k}{m g}}\right)-t \sqrt{\frac{k g}{m}}\right)\)
\(a(t)=-g \operatorname{sech}^2\left(\operatorname{arctanh}\left(v_0 \sqrt{\frac{k}{m g}}\right)-t \sqrt{\frac{k g}{m}}\right)\)
\(s(t)=s_0-\frac{m \ln \left(\cosh \left(\operatorname{arctanh}\left(v_0 \sqrt{\frac{k}{m g}}\right)-t \sqrt{\frac{k g}{m}}\right)\right)}{k}\)
Basics
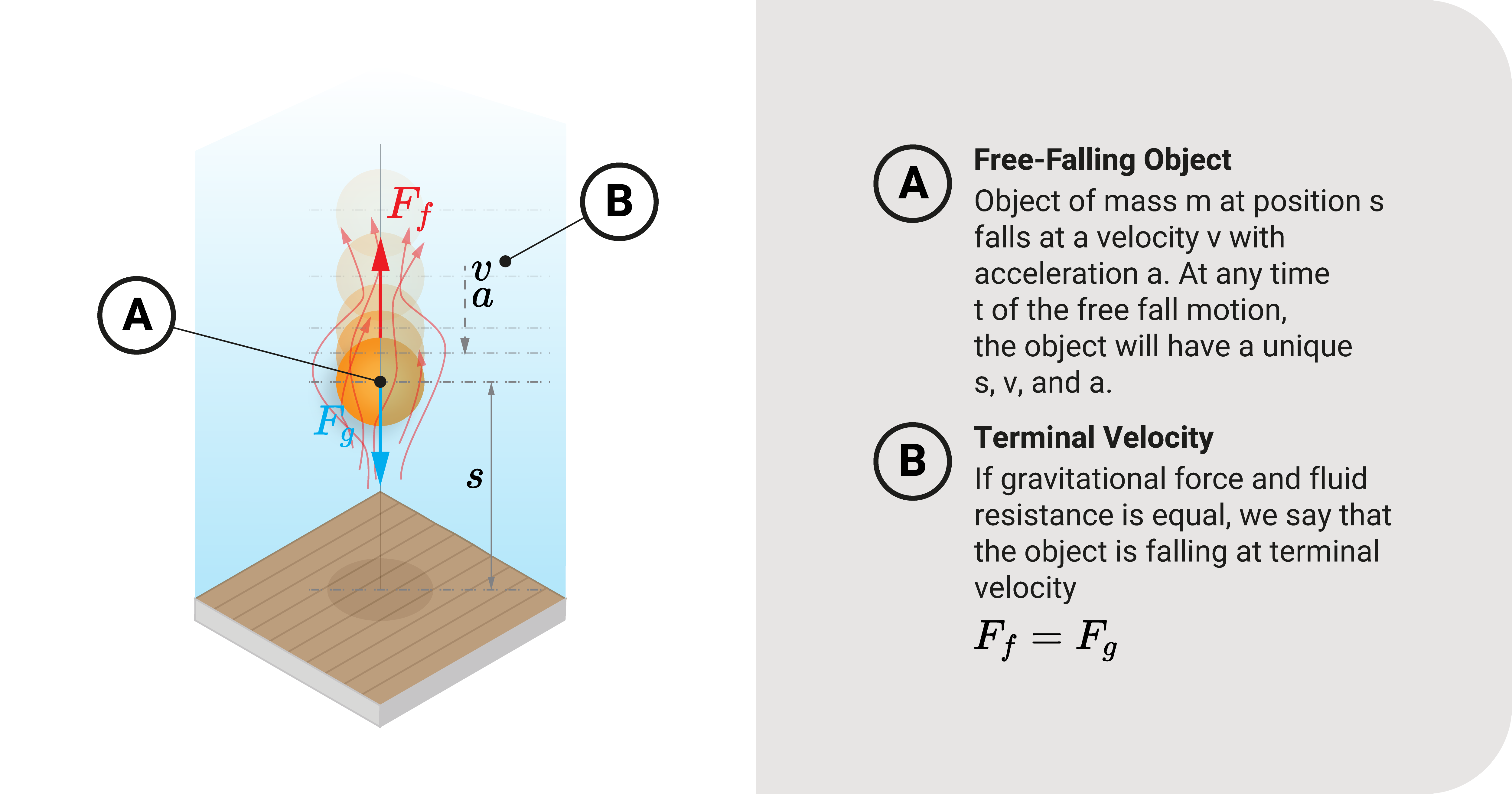
Recall that the falling object will experience two forces: gravitational pull and fluid resistance. The former force usually remains constant while the latter builds up as the object gets velocity \(v\).
Eventually, there will be a point in time wherein these two forces will be equal. The resistance force has gained enough magnitude to equate to gravitational pull. From Newton's Laws, these forces will cancel out, and no acceleration will occur.
With no acceleration, the falling object will never gain speed anymore. It is still falling, but it will never get faster.
This speed the falling object reaches when \(F_g\) and \(F_f\) are equal is what we call the terminal velocity.
Mathematically speaking, we can express it by taking the limit of the v-t function to infinity:
\(\lim _{t \rightarrow+\infty} v(t)=\lim _{t \rightarrow+\infty}\left(\sqrt{\frac{m g}{k}} \tanh \left(\operatorname{arctanh}\left(v_0 \sqrt{\frac{k}{m g}}\right)-t \sqrt{\frac{k g}{m}}\right)\right)=-\sqrt{\frac{m g}{k}}\)
\(v_t=-\sqrt{\frac{mg}{k}}\)
- \(v_t\) is the terminal velocity
- \(m\) is the object's mass
- \(g\) is the acceleration due to gravity
- \(k\) is the proportionality constant (drag)
Illustration
To illustrate this phenomenon, below is an example plot of the motion functions with the following parameters:
- The falling object has a mass of 65 kg \(m\)
- It has an initial velocity of \(v_0=0\)
- It came from a height of 800m, initial position \(s_0\)
- Gravitational acceleration is 9.81 \(\frac{m}{s^2}\)
- Variable \(k\) is equal to 0.035
Let's say that this object falls forever. There would be a point where the velocity would remain constant at around 135 m/s (see v-t graph) around 90 seconds after dropping it. At this point, we have reached the terminal velocity.
Interestingly, in our acceleration-time graph, acceleration will eventually become zero around the same time. It implies that the velocity would not gain any more speed as it falls, which we can see in our v-t graph.
Summary
A falling object will experience two forces: gravitational pull \(F_g\) and fluid resistance \(F_f\). The former force usually remains constant while the latter builds up as the object gets velocity \(v\).
Eventually, there will be a point in time wherein these two forces will be equal. The resistance force has gained enough magnitude to equate to gravitational pull.
There will be no acceleration at this point, and the falling object will never gain speed anymore.
This speed the falling object reaches when \(F_g\) and \(F_f\) are equal is what we call the terminal velocity.
It is equal to \(v_t=-\sqrt{\frac{mg}{k}}\) where \(v_t\) is the terminal velocity, \(m\) is the object's mass, \(g\) is the acceleration due to gravity, and \(k\) is the proportionality constant (drag)




.png)
