One of the fundamental forces of nature is the gravitational force. In this post, we'll explore more about it.
Basics
Let's start expanding what gravitational force \(F_g\) is. In elementary Physics, we may quickly refer to it as weight. From Newton's second law of motion, we can express gravitation force as:
\(F_g=mg\)
- \(m\) is mass
- \(g\) is the acceleration due to gravity
Mass \(m\) is a scalar quantity; however, the variable \(g\) is an acceleration vector quantity which means it has both magnitude and direction. As such, the sign of \(g\) matters, which would depend on the situation. On Earth, \(g\) is around \(9.81 \frac{m}{s^2}\) or \(32.1 \frac{ft}{s^2}\).
Deriving Acceleration Due to Gravity
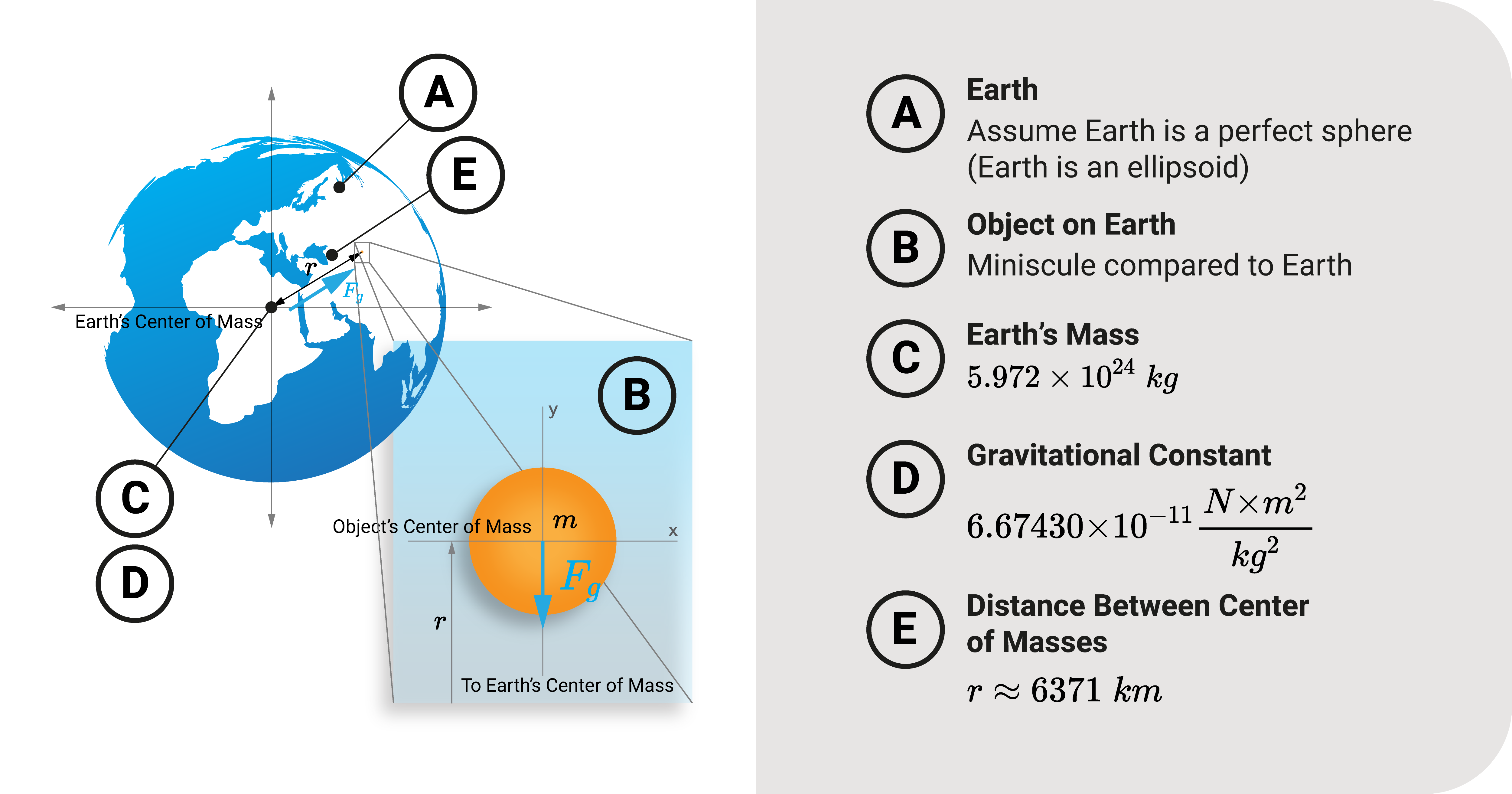
Have you ever wondered how acceleration \(g\) is derived?
To answer this question, we recall what gravity is. By its essence, it is simply an invisible pulling force \(F_g\) between objects.
We measure this pulling force using Newton's Law of Universal Gravitation which states that:
\(F_g=\frac{G m_1 m_2}{r^2}\)
- \(G\) is the gravitation constant (6.674×10−11 \(m^3 \cdot kg^−1 \cdot s^−2\))
- \(m_1\) is the mass of the first object
- \(m_2\) is the mass of the second object.
- \(r\) refers to the distance between the center of masses between the two objects.
Let's consider the interaction between a random body with mass \(m_1\) and our planet Earth with mass \(m_2\). Our goal is to try and solve \(F_g\)
- Our object has a mass \(m\) while Earth has a mass equal to \(5.972 × 10^{24} kg\). Due to gravity, these objects will tend to pull toward each other.
- For \(r\), we determine the distance between the center of masses between Earth and the object. Ideally, it would be the sum of Earth's equivalent radius (6371 km) and the extra distance needed to reach the object's center of mass; however, the latter is so minuscule compared to the Earth's radius that it bears no significant impact on the computation of the pulling force; hence, we'll assume that \(r\) is equal to 6371 km.
With these values, we can say that the pulling force between Earth and the object is:
\(F_g=\frac{\left(6.674 \times 10^{-11}\right)\left(5.972 \times 10^{24}\right)}{(6371 \times 1000)^2} \times m\)
Evaluating this expression will yield:
\(F_g \approx 9.81 \times m\)
The computed figure, 9.81, is a conservative acceleration value due to gravity \(g\) in SI units. It's how we arrived at our constant value.
From this discussion, the primary variables affecting acceleration due to gravity are the mass of the objects and the center-to-center distance between them. As such, the constant 9.81 only applies to an object here on Earth.
In addition, our derivation assumes that the Earth is a perfect sphere, but it is an oblate spheroid. It implies that \(r\) varies depending on where you are on Earth. In practice, we use the traditional value of \(9.80665 \frac{m}{s^2}\).
Summary
Gravitational force \(F_g\) deals with the pulling force between two objects due to gravity.
In elementary Physics, it is weight.
Mathematically, it is equal to the product of scalar mass \(m\) and vector acceleration due to gravity \(g\)
On Earth, \(g\) is around \(9.81 \frac{m}{s^2}\) or \(32.1 \frac{ft}{s^2}\).
We derive this constant \(g\) from Newton's Law of Universal Gravitation which states that: \(F_g=\frac{G m_1 m_2}{r^2}\). \(G\) is the gravitation constant (6.674×10−11 \(m^3 \cdot kg^−1 \cdot s^−2\)), \(m_1\) is the mass of the first object, \(m_2\) is the mass of the second object, and \(r\) refers to the distance between the center of masses between the two objects.
From this, the primary variables affecting acceleration due to gravity are the mass of the objects and the center-to-center distance between them.
It implies that \(g\) will change if we are on a different planet and closer or farther to the object's center. In practice, we use the traditional value of \(9.80665 \frac{m}{s^2}\) here on Earth.



