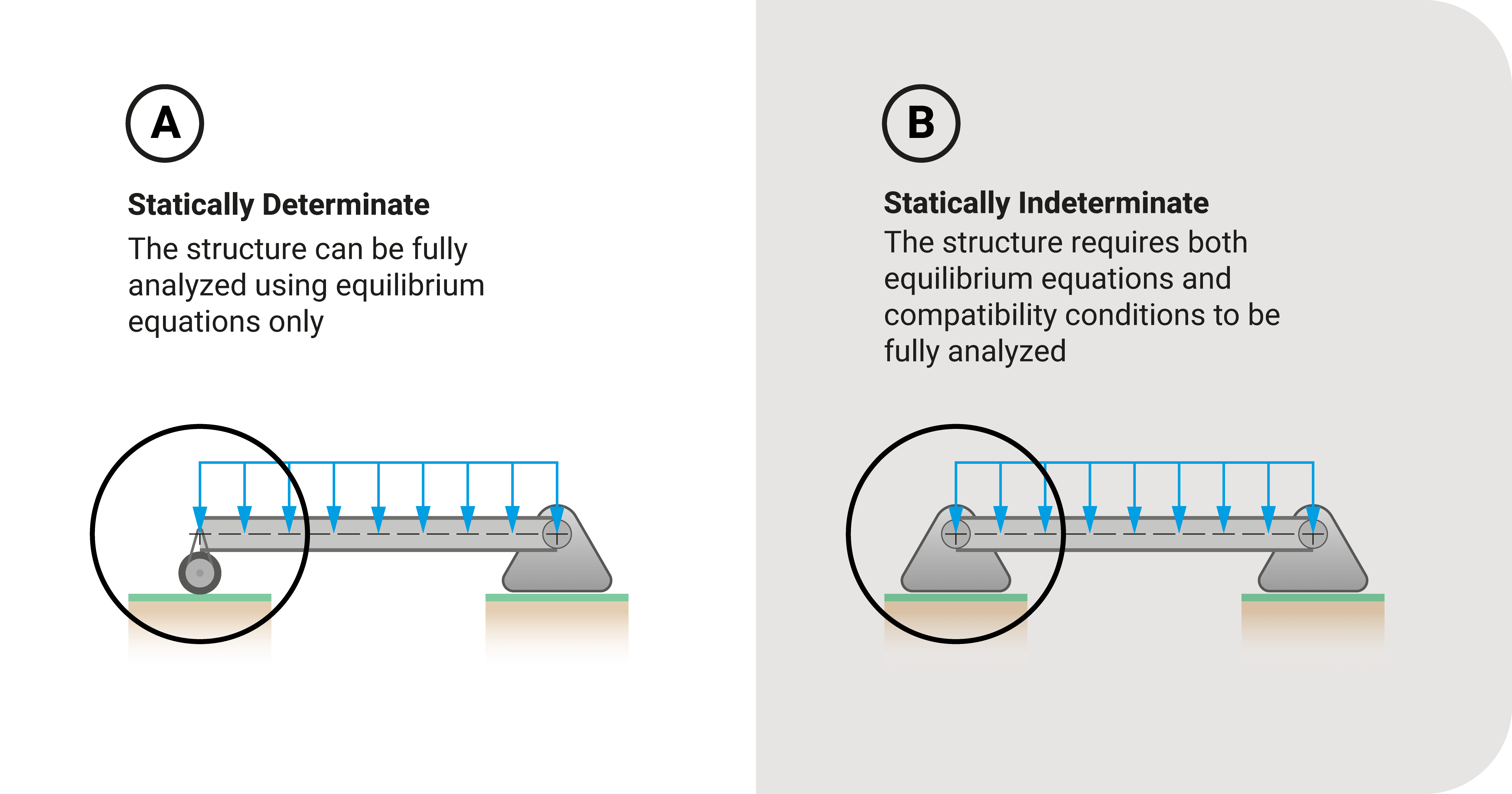
When a structure experiences static loads, it can either be statically determinate or indeterminate. The former can be analyzed using static equilibrium equations ONLY, while the latter requires more than those equations.
How do we know if a structure is such? We first introduce two concepts: the Number of Unknowns \(N_u\) and the Number of Known Conditions \(N_k\) of a structure.
Number of Unknowns
The number of unknowns \(N_u\) refers to the number of reactions and internal forces we need to solve. It is the sum of (1) external reaction components \(r\) and (2) internal force components.
Below is a table of unknowns depending on the type of structure. The variable \(m\) refers to the number of members in the model.
Number of Known Conditions
The number of known conditions \(N_k\) refers to the number of equations we can use to solve the structure. It is the sum of (1) equilibrium equations and (2) conditional equations due to internal connections \(e_c\).
Below is a table of these conditions depending on the type of structure. The variable \(j\) refers to the number of joints in the model.
How to Classify Determinacy?
To classify if a structure is determinate or not, we need to compare the number of unknowns \(N_u\) and the number of known conditions \(N_v\):
- If \(N_u = N_k\), the number of unknowns is the same as the number of known equations. The equilibrium principle is sufficient to solve the structure; hence, it is determinate.
- If \(N_u > N_k\), there are more unknowns than known equations. We will need more equations to solve the structure; hence, it is indeterminate.
- If \(N_u < N_k\), there are fewer unknowns than known equations. It violates external stability; hence, the structure is externally unstable.
Degree of Indeterminacy
If a structure is indeterminate, how many more equations do we need to study its behavior? The degree of indeterminacy \(D_i\) tells us exactly that. It's simply the difference between the unknowns and known equations:
\(D_i = N_u -N_k\)
Again, there are three possible scenarios of \(D_i\). For example,
- If we have a \(D_i\) of two, the number of unknowns is greater than the number of known conditions. We would need two more equations to solve the structure.
- If \(D_i\) is equal to zero, then we won't need additional equations to solve it; hence, we can say that it is determinate.
- Lastly, if \(D_i\) is a negative number, the number of unknowns is less than the number of known conditions. Meaning it would violate the stability of the structure.
We can summarise this example as follows:
- \(D_i > 0\) means the structure is indeterminate; the number tells us how many additional equations we need more
- \(D_i = 0\) means the structure is determinate
- \(D_i < 0\) means the structure is externally unstable
This equation can also be an excellent strategy to determine whether a structure is determinate or indeterminate rather than comparing \(N_u\) and \(N_k\).
Summary
Statically determinate structures can be analyzed using static equilibrium equations only. Conversely, statically indeterminate structures cannot be analyzed using such equations only.
The number of unknowns \(N_u\) refers to the number of reactions and internal forces of the structure we need to solve.
The number of known conditions \(N_k\) refers to the number of equations we know to solve the structure.
Comparing \(N_u\) and \(N_k\) will give the determinacy \(D\) of the structure.
The degree of indeterminacy \(D_i\) can answer the number of additional equations needed for indeterminate structures and is equal to \(D_i = N_u - N_k\).
The equation \(D_i = N_u - N_k\) can help us tell whether the structure is determinate, indeterminate, or unstable.







