"Integral" means "to make whole or complete." That's precisely what the idea of integration is doing. In this post, we'll explore the essence behind this operation.
Elementary Geometry is Limited
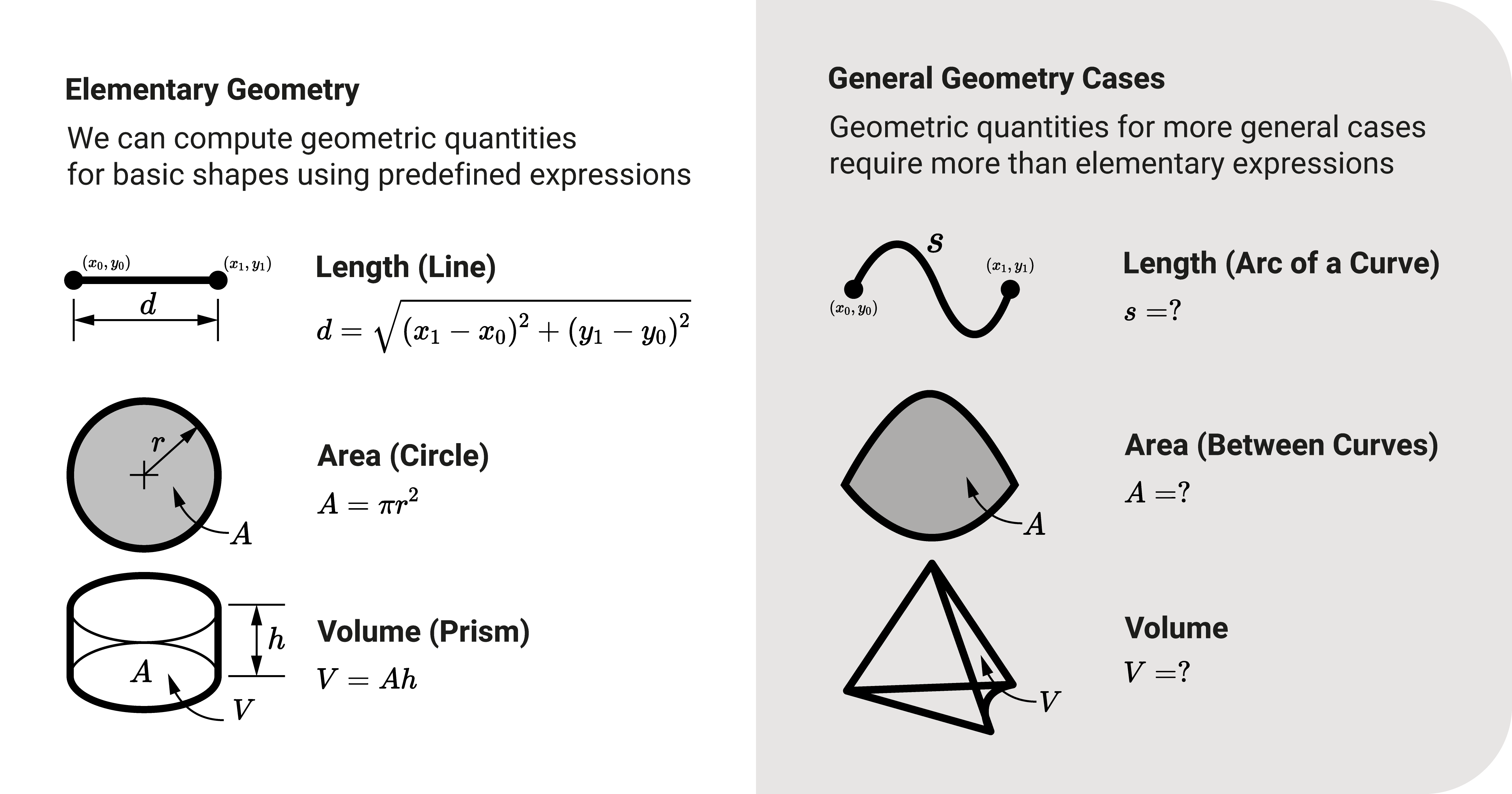
To understand the meaning of an integral, we have to look at what it is trying to solve in the first place.
Say we have the following geometric problems:
- Find the length of a line between two points.
- Find the area of a typical section, like a closed rectangle
- Find the volume of a solid with a known cross-sectional shape, like that of a cylinder.
Typically, we can solve these problems using analytic or solid geometry principles. To solve the math problems above:
- We use the distance formula to solve the distance between two points along a line.
- If we want to solve the area, we solve using pre-defined equations in geometry. In our closed rectangle, it would be base times height.
- If we want to solve for the volume, we use Cavalieri's theorem to get it.
As much as these ideas help us find an answer, there is a problem. These solutions are limited. They do not encompass a wide variety of situations we may face. For example, we may encounter the following issues too:
- Find the length of a curve, say a curved portion or an arc.
- Find the area underneath a curve boundary
- Find the volume of a solid with an irregular cross-sectional shape.
From these problems, we can already see the limitations of our pre-defined formulas and equations. We cannot simply use the distance, area, or volume formulas to arrive at an answer.
The best thing we can do in using Elementary geometry is to approximate an answer.
Approximating a Solution

How do we approximate a solution? We subdivide the object into many recognizable parts and then take the sum of each division. In our problems:
- We can divide the curve into multiple lines and solve each using the distance formula. Afterward, we take the sum of each line to get an answer.
- We split the area underneath the curve boundary into many parts, say multiple rectangles. We solve the area of each rectangle, then take the sum to get the total area.
- We subdivide the volume into numerous solids. Solve for the volume of each division, then sum each part to get the solid's volume.
How Do We Find the Exact Solution?
When we approximate by this method, we can have some idea of the answer is; It is an excellent method to gain a ballpark, but again, it is only an approximation. How do we find the precise solution to the problem?
Let's discuss what does affect the approximation's accuracy:
- The shape of the division
- The number of divisions
- The size of the divisions
Taking our length of an arc example, we can have a more precise answer if we have more line divisions with consistent length. Having more parts will mean smaller dimensions each.
If we want to find the exact answer, the dimensions of these parts will have to be small. In Math, we can represent these small changes: the differential.
This differential represents the infinite and tiny divisions of our approximation.
The Meaning Behind the Integral

Now that we have a differential part, we can find the correct answer to our geometric problems. What's left is to take the sum of all differentials just like we did with the approximation process. But how do we exactly do that?
That's where integration comes in. It's a process where we find the whole from the parts.
With this idea, integration breaks the limitations of Elementary geometry. We can solve a wide array of geometric problems when using integration.
In the following sections, we'll explore how to use it to find:
Summary
Elementary geometry solutions are great for solving different problems but are limited.
Usually, when facing a geometric problem outside its limits, we can only approximate it.
We approximate by taking the object and dividing it into many recognizable parts we can solve using Elementary geometry.
The approximation becomes better if the divisions are infinite and tiny, which we represent using differentials.
We take the sum of these differentials through integration - "the process of finding the whole from many parts."






