The virtual work method (also known as the unit-load method) is one of the practical and flexible methods for solving deflections. This method allows you to solve for the deflections of beams, frames, and trusses; hence, it is a must-know procedure.
Before discussing the virtual work equation, we must familiarize ourselves with a special notation for unit loads and couples:
Unit Load
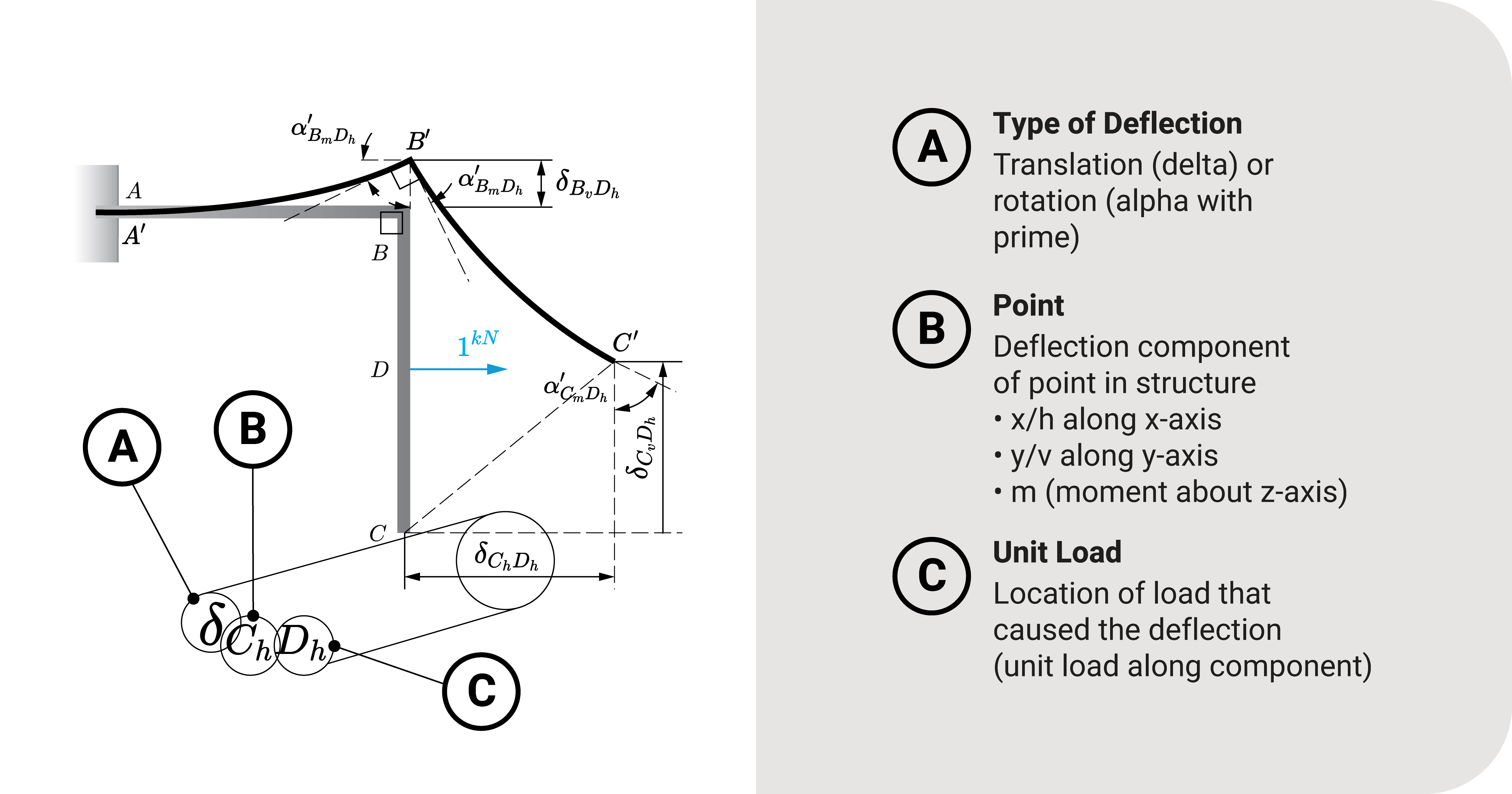
Say we have a frame with a unit load of \(1kN\) acting to the right at point \(D\). It causes the structure to deflect, as shown.
To represent the deflection of this structure due to the unit load, we use the following:
- Linear translation \(\delta\).
- For horizontal components, it is either \(\delta_h\) or \(\delta_x\)
- For vertical components, it is either \(\delta_v\) or \(\delta_y\)
- Angular translation / Rotation \(\alpha^{'}\) or \(\alpha^{'}_{m}\)
The translation is the lowercase Greek letter delta \(\delta\), while rotation is the Greek letter alpha \(\alpha\) with an apostrophe.
The subscript naming convention consists of two components: (1) the type of deflection and (2) the unit load that causes it.
Let's go back to our frame and name the horizontal deflection at \(C\), which would be \(\delta_{C_hD_h}\). The first part \(\delta_{C_h}\) means we are identifying the horizontal deflection at \(C\). The second part, Dh, refers to the unit horizontal load at D, which caused that deflection.







