The parabola is a conic section in which its locus is the set of all points equidistant to a fixed point called the focus and a fixed line called the directrix. 
WeTheStudy lets you connect ideas
Learn more

The parabola is one of the primary conic sections. In any engineering or mathematics application, we'll see a lot of applications:

  • Describing projectile trajectory
  • Designing vertical curves in roads and highways
  • Making reflectors and telescope lenses.

These are a few examples of its many uses. For now, let's learn more about the basic geometry of the parabola:

Locus Definition

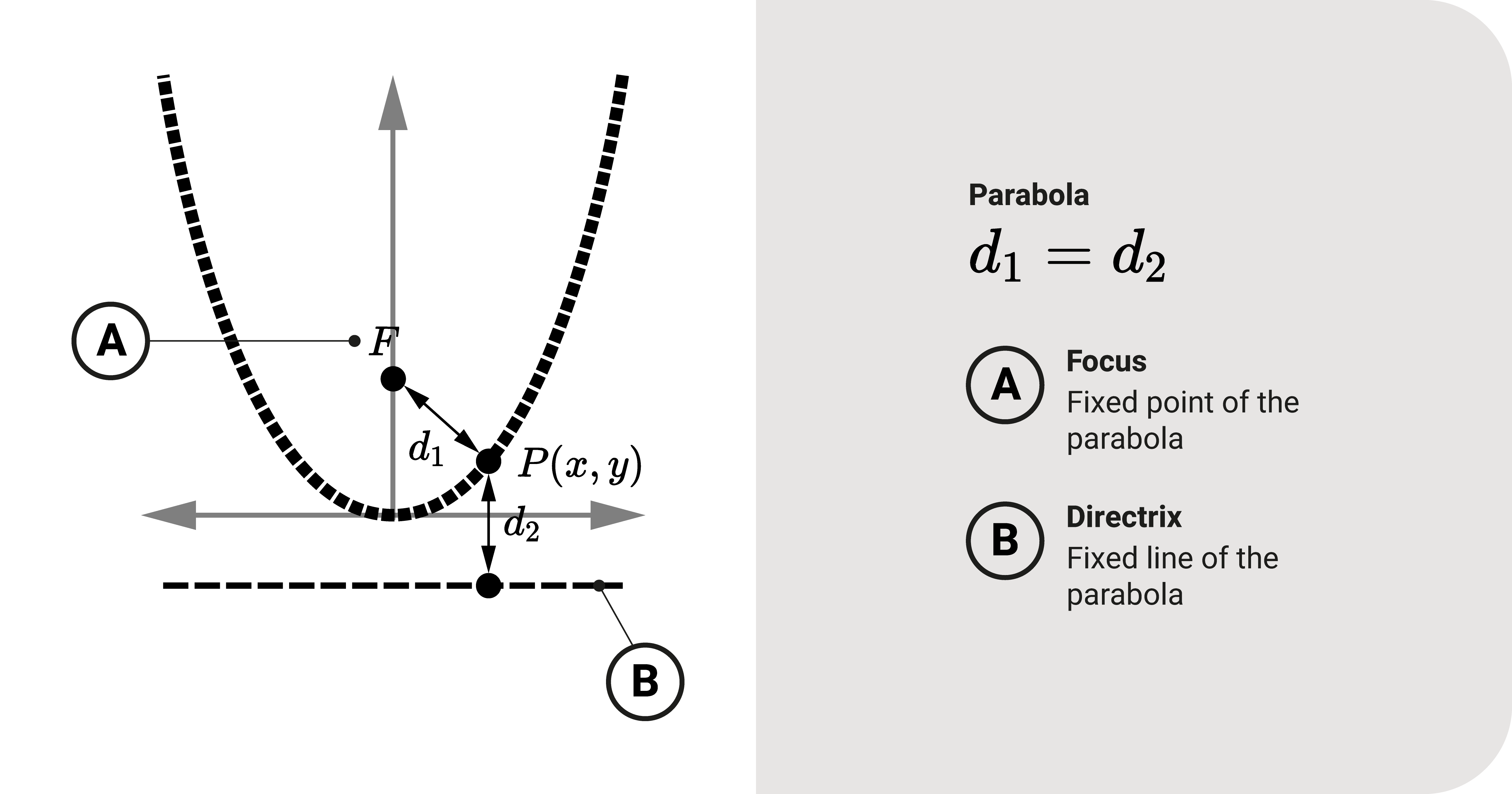
Basic geometry of a parabola

At its basic, it is a set of all points that is equidistant to:

  • A fixed point \(F\) called the focus, 
  • A fixed line called the directrix. 

To expand, let's consider a point \((x, y)\) as shown in the figure. The distance \(d_1\) between this point and \(F\) should be equal to its perpendicular length \(d_2\) to the directrix.

Want to access the remaining content?
You're a Member!
Click to expand on exclusive content
Want to access the remaining content?

Become a Member

When you sign-up and subscribe to WeTheStudy, you’ll get the following benefits:

No ads! (yey!)
Complete access to all articles
Ability to track your progress in the tree

SIGN-UP

Complete Your Checkout

When you complete your account, here are the following benefits:

No ads! (yey!)
Complete access to all articles
Ability to track your progress in the tree

PROCEED CHECKOUT

Parts of a Parabola

The parabola has certain notable parts to consider:

Parts of a Parabola

  1. Vertex \(V\) is a point halfway between the focus \(F\) and the directrix. It has the coordinate \((h, k)\).
  2. Focus \(F\) is a fixed point at which \((x, y)\) is equidistant to that of the directrix.
  3. Directrix is a fixed-line at which \((x, y)\) is equidistant to that of the focus.
  4. Directed distance, \(a\) is the halfway distance between the directrix and \(F\).
  5. Axis is the line that passes through \(V\) and \(F\). Depending on the orientation, it may be vertical, horizontal, or inclined. In addition, the graph is symmetrical about this axis.
  6. A focal chord is any line segment that passes through \(F\) and has its endpoints on the parabola.
  7. The Latus Rectum is a focal chord that is perpendicular to the axis. It has a length equal to \(4a\).

Summary

The parabola is a set of all points equidistant to a fixed point \(F\) called the focus and a fixed line called the directrix. 
The parabola has certain notable parts: vertex, focus, directrix, directed distance, axis, focal chord, and the latus rectum.

No ads?

Tree Navigation

See how this article relates to other ideas
Children
No children (yet)
Siblings

#

2

Orienting the Parabola

The parabola can be oriented in different ways. The most common orientations are vertical and horizontal parabolas. We'll explore the properties of each in this post.

Parent

#

1

Parabola

The parabola is one of the conic sections. Let's explore its definition, shape, and geometry through the following series.

Connections
No connections (yet)
Created On
June 5, 2023
Updated On
February 23, 2024
Contributors
Edgar Christian Dirige
Founder
References

WeTheStudy original content

Revision
1.00
Got some questions? Something wrong? Contact us
This account is currently deactivated due to a
failed payment. Update your payment method now