Conic sections are, without a doubt, an essential topic. There are four of these: the circle, parabola, ellipse, and the hyperbola.
These geometric shapes have countless applications – to describe projectile motion, to explain how planets move, to design roads and highways, to build structures, and more.
The Double-Napped Cone
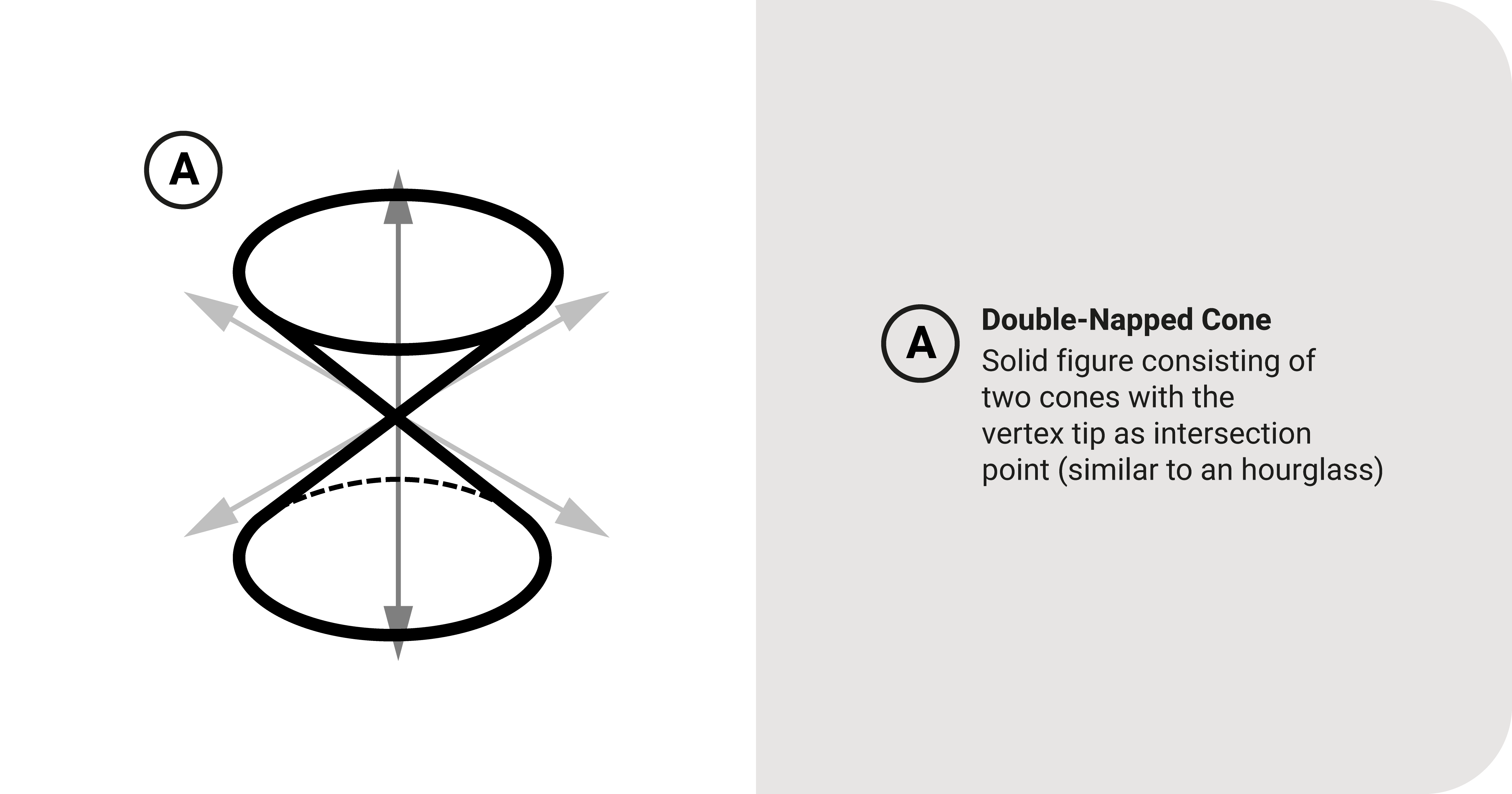
Let's ask, "Why are they called conic sections?"
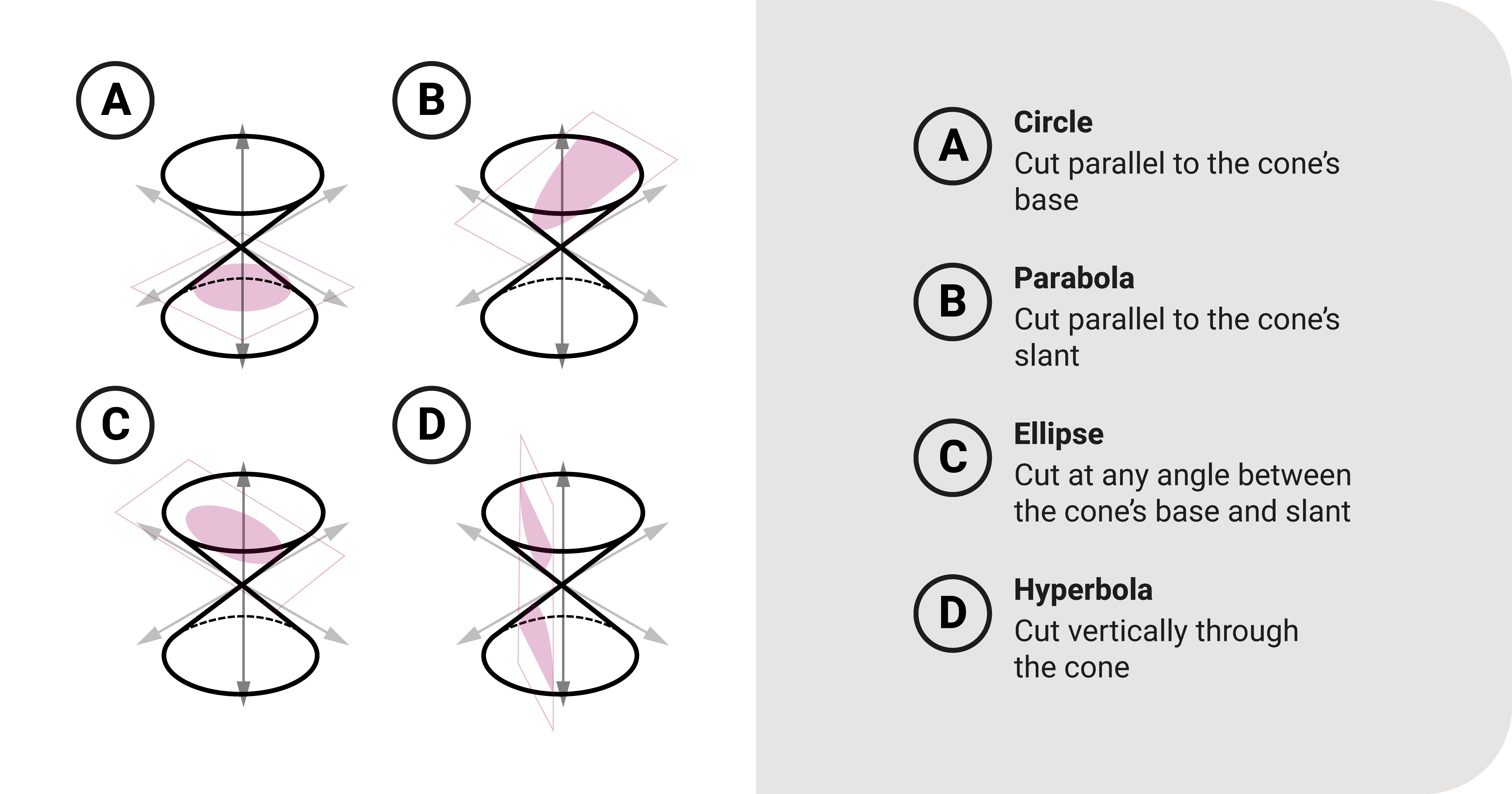
Consider a double-napped cone in space. Let's pass a plane through this cone at various angles and get the intersecting section between the two:
- If we pass the plane parallel to the base of a cone, then the intersection is a circle.
- If we pass the plane parallel to the slant of a cone, it is a parabola.
- If we pass the plane at any angle (other than those described in a circle or parabola) through one cone, it is an ellipse.
- If we pass the plane vertically through the two cones, it is a hyperbola.
From this demonstration, we can say that these shapes are conic sections because we can construct it by passing sections through this double-napped cone.
Algebraically speaking, all of these sections have the general form:
\(A x^2+B x y+C y^2+D x+E y+F=0\)
- \(A\), \(B\), \(C\), \(D\), \(E\), and \(F\) are constants
- \(x\) is an independent variable
- \(y\) is a dependent variable
Suppose we pass the plane through the meeting point of the two cones; what is the resulting section? It would be just a simple point that we call a degenerate conic.
Conic Sections as Locus
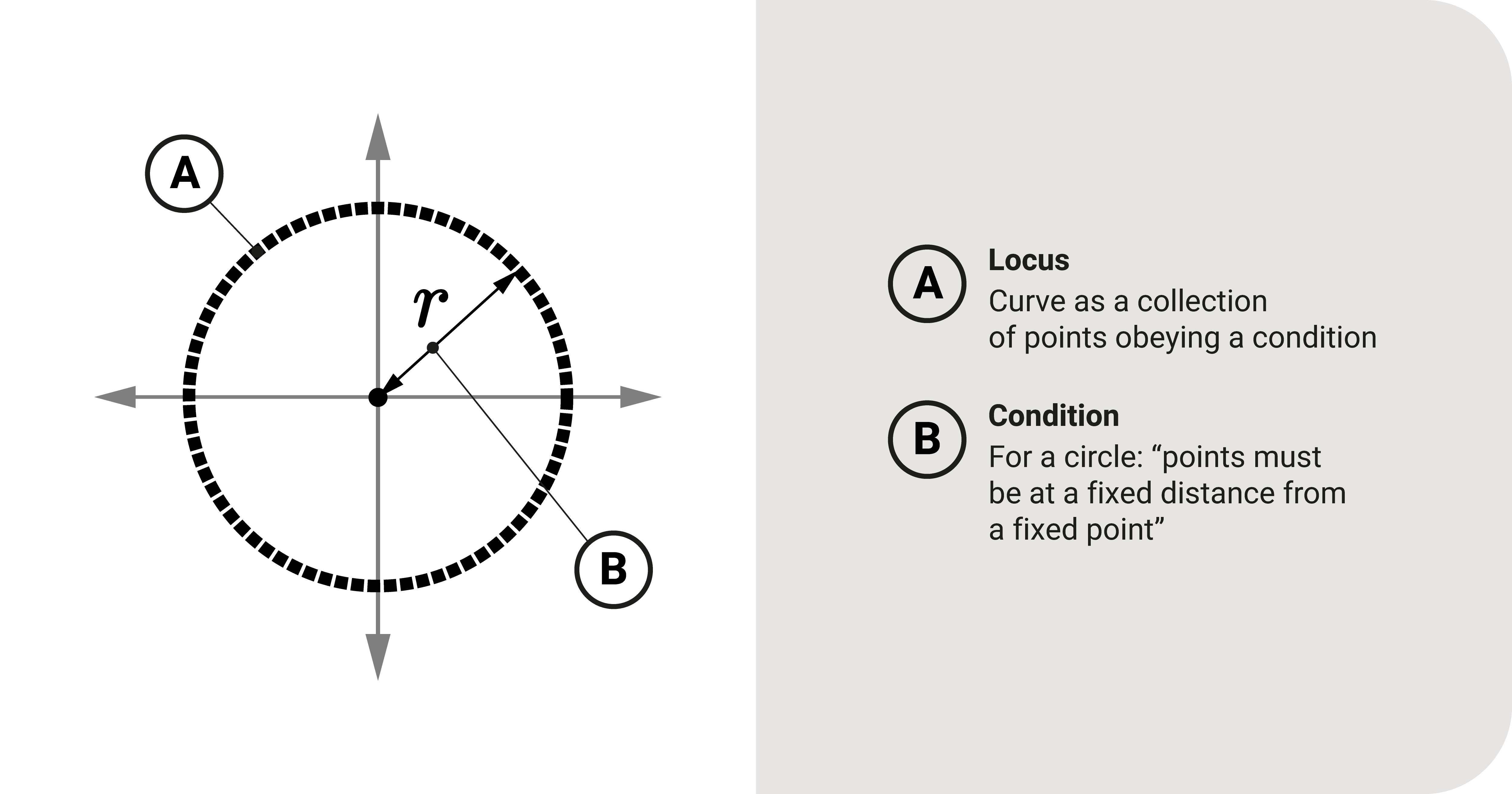
We can describe conic sections as a locus – a set of all points obeying a condition which could be anything like "fixed from a point," "n units from a point," "at a distance three from a plane," and more.
To further explain it, we need to visualize a curve as an endless series of points that move along a specific path. For example:
- A circle is a curve in which it is a collection of points that obeys a condition: equidistant to a fixed point we call the center.
In the following posts, we'll explore more of this locus-based definition of the different conic sections.
Summary
There are four conic sections: the circle, parabola, ellipse, and the hyperbola.
We can derive these sections from the double-napped cone.
All of these sections have the general form: \(A x^2+B x y+C y^2+D x+E y+F=0\)
We can describe conic sections as a locus – a set of all points obeying a condition.





