Deriving Virtual Work Due to Axial Strains

Let's consider a simple triangular truss. Our goal is to determine \(U_{s_\delta}\), which is the product of fictional internal forces and actual strains, so that we can arrive at a definite expression to solve for the deflection of axial structures.

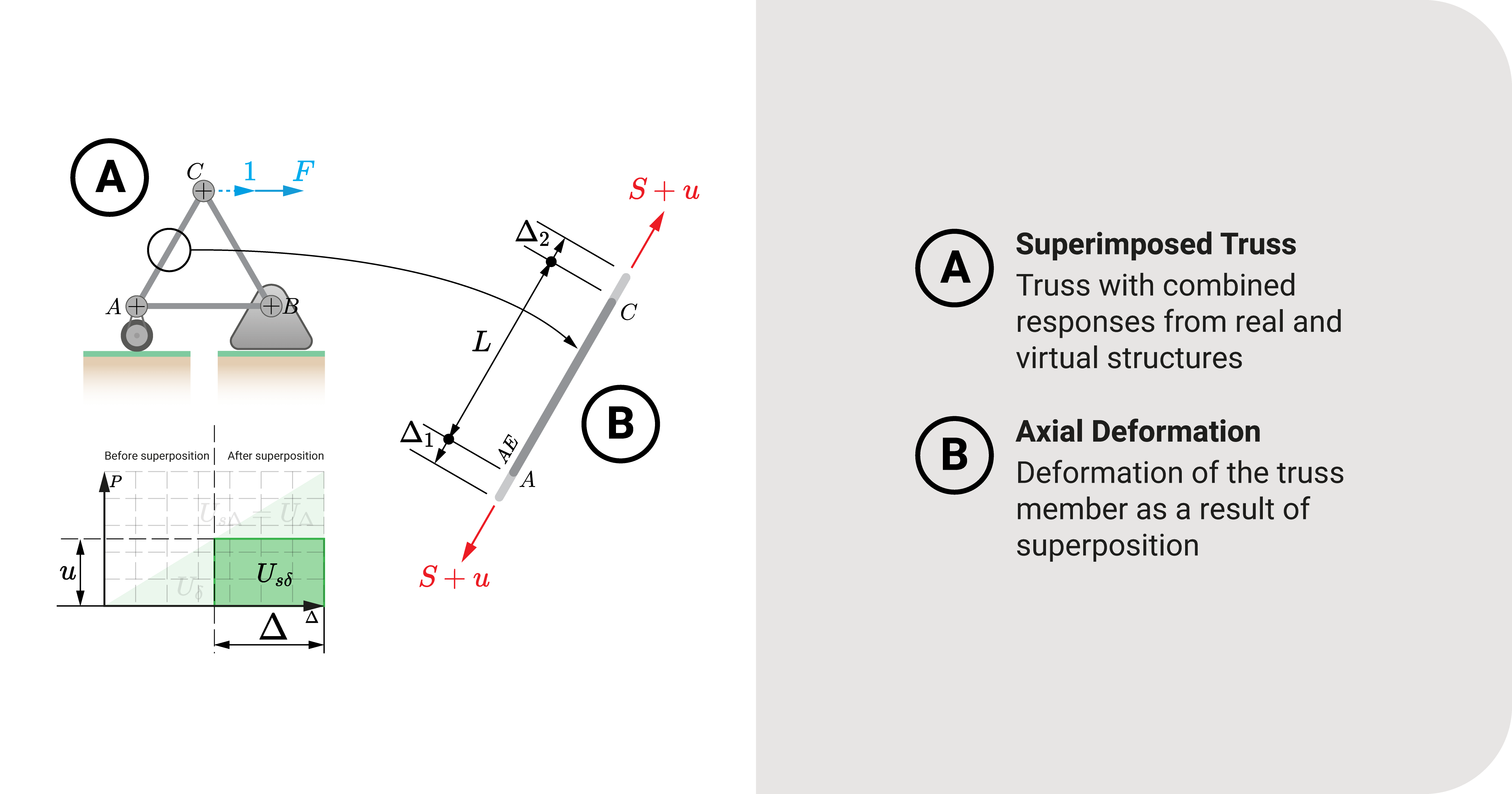
It is equal to the area underneath the graph shown in the figure. Symbolically, we can express it as: 

Equation 1: \(U_{s_\delta}=\int{u}d\Delta\)

• The variable \(u\) refers to the fictional internal bar forces caused by the unit loadings.
• \(d\Delta\) is the real strain the bar experiences of length \(L\) under superimposed loadings.

If we investigate \(d\Delta\) further using the exact figure, it is the sum of \(d\Delta_1\) and \(d\Delta_2\). Any Strength of Materials course will tell you that axial deformation \(d\Delta\) is equal to:

Equation 2: \(d\Delta=\frac{S}{AE}dx\)

Substituting this to Equation 1:

Virtual Work - Axial Strains: \(U_{s_\delta}=\int\frac{Su}{AE}dx\)

Key Idea: Virtual Work Due to Axial Strains

Now, if we equate the virtual work general equation and \(U_{s_\delta}\), we can arrive at the equations we will use to solve for the deflection due to axial strains:

Virtual Work - Axial Strains - Horizontal Translation: \(1{\times}\Delta_h=\int_{x_1}^{x_2}\frac{Su_h}{AE}dx\)

Virtual Work - Axial Strains - Vertical Translation: \(1{\times}\Delta_v=\int_{x_1}^{x_2}\frac{Su_v}{AE}dx\)

Virtual Work - Axial Strains - Rotation: \(1{\times}\theta=\int_{x_1}^{x_2}\frac{Su_\alpha}{AE}dx\)

Here is the meaning of the variables in those equations:

• The unit force or couple represents the fictional unit load applied to the virtual structure.
• \(\Delta\) means translation of joint.
• \(\theta\) represents the rotation of a specific member.
• \(S\) is the internal bar force caused by the superimposition of loadings (may be a function of position \(x\)).
• \(u_v\), \(u_h\), \(u_\alpha\) are the internal bar forces generated by the unit loading of the virtual structure.
• \(AE\) is also known as axial rigidity
• Limits \(x_1\) and \(x_2\) are the member's local start and end coordinates, respectively.

These equations consider the effect of members with varying axial loads and cross-sections; however, in most real-life situations, these properties, \(S\), \(u\), \(A\), and \(E\) throughout \(x\) are constant. In these situations, we can simplify the equations as follows:

\(1{\times}\Delta_h=\sum_{i=0}^{n}\frac{S_iu_{h_i}L_i}{A_iE_i}\)

\(1{\times}\Delta_v=\sum_{i=0}^{n}\frac{S_iu_{v_i}L_i}{A_iE_i}\)

\(1{\times}\theta=\sum_{i=0}^{n}\frac{S_iu_{\alpha_i}L_i}{A_iE_i}\)

When dealing with truss members, one important thing to note is that the expression we use to find for rotation refers to the truss member (not the joint). We'll expound on this using an illustrative problem later on.

‍Summary

Let's summarize:

The expression for the superimposed fictional strain energy due to axial strains is \(U_{s_\delta}=\int\frac{Su}{AE}dx\).

The equations we will use to solve for the deflections are the following: (1) \(1{\times}\Delta_h=\int_{x_1}^{x_2}\frac{Su_h}{AE}dx\), (2) \(1{\times}\Delta_v=\int_{x_1}^{x_2}\frac{Su_v}{AE}dx\), and (3) \(1{\times}\theta=\int_{x_1}^{x_2}\frac{Su_\alpha}{AE}dx\).

If \(S\), \(u\), \(A\), and \(E\) are constant, we can further simplify such equations as (1) \(1{\times}\Delta_h=\sum_{i=0}^{n}\frac{S_iu_{h_i}L_i}{A_iE_i}\), (2) \(1{\times}\Delta_v=\sum_{i=0}^{n}\frac{S_iu_{v_i}L_i}{A_iE_i}\), and (3) \(1{\times}\theta=\sum_{i=0}^{n}\frac{S_iu_{\alpha_i}L_i}{A_iE_i}\)