Multiplication is an essential skill to learn. Despite having calculators and computers to do the multiplying for us, learning how to do it by hand is an asset, but did you know that there are multiple ways to multiply numbers?
To illustrate, let's find the product of 125 (multiplicand) x 42 (multiplier) using different methods:
Column Method

This method is probably the usual way of learning multiplication.
- First, align the multiplicand and the multiplier so each place value is on the same column. The ones are in the same column, then the tens, the hundreds, thousands, millions, etc.
- Next, you multiply each place value of the multiplier by each place value of the multiplicand.
- Align all the products based on their place values and add to get the final product, which is 5250.
Box Multiplication
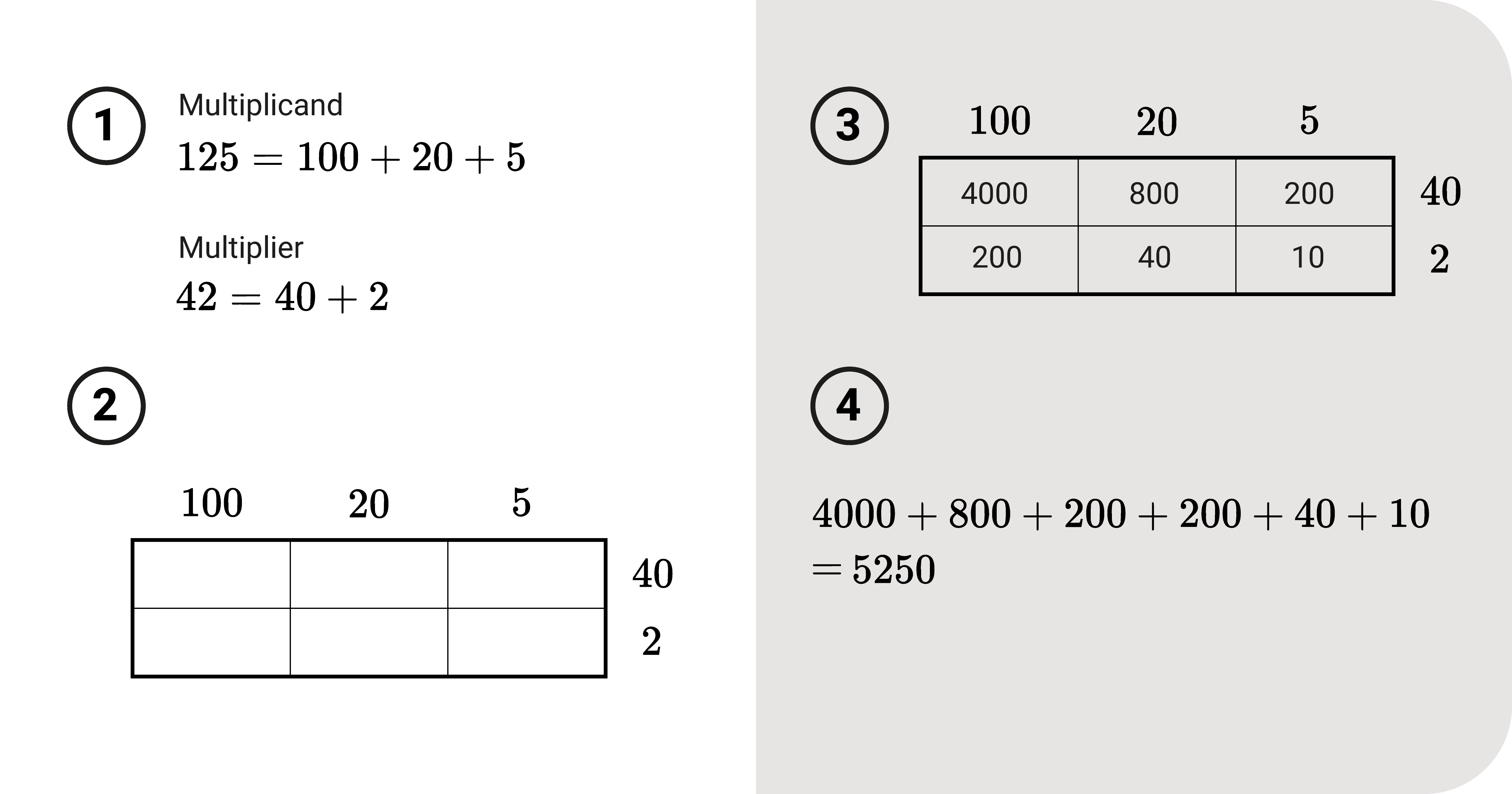
Another method is the box or grid method. To illustrate,
- First, break down the numbers as a sum (or addends) based on their place value. In our example, 125 is 100+20+5, and 42 is 40+2. Three addends for 125 and two addends for 42.
- Afterward, draw a grid (hence the name). The number of columns is the number of addends of the multiplicand, while the number of rows is the number of addends of the multiplier. In this case, we have three columns and two rows. Label each column by the addends of the multiplicand and label each row by the addends of the multiplier (similar to the diagram). Column 1 is 100, Column 2 is 20, and Column 3 is 5. Row 1 is 40, and Row 2 is 2.
- Multiply each row and column to one another and place the product on their intersection.
- Finally, add all the results inside the box to get the final product, 5250.
Stick Multiplication
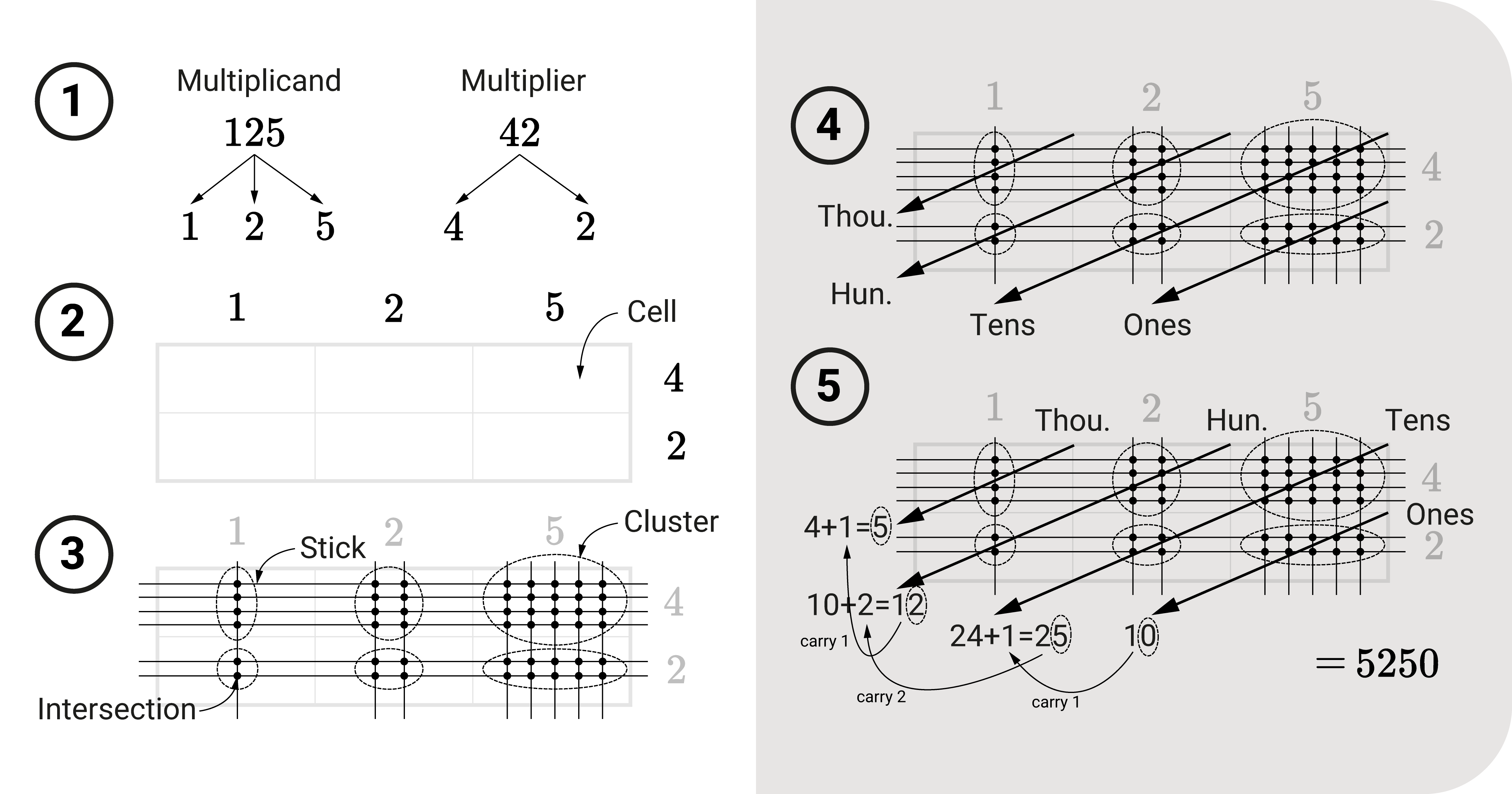
If we want to multiply numbers with a visual aid, we'll be interested in Stick Multiplication.
- Break down the multiplicand and multiplier into numbers. For 125, it would be 1, 2, and 5 (3 numbers). For 42, it would be 4 and 2 (2 numbers).
- Imagine a grid (similar to the box method) with the number of columns and rows equal to the number of broken-down digits. In our example, it would be 3x2. Label each column and row with the broken-down numbers.
- Draw "sticks" that would run across the grid based on the value of the digits. For the values in the column, draw one vertical line on the first column, two on the next, and five on the last column. Then, for 42, draw four horizontal lines on the first row, then two lines on the final. These lines must intersect at points in each cell of the table. Each group of points in each cell is a cluster.
- Imagine a diagonal line (from top-right to bottom-left) running through the table cell. See the grid to visualize these diagonals. Each of these will group a cluster of points. These diagonals represent the place value of the product (ones, tens, hundreds, thousands, and so on).
- Count the number of points in each cluster per diagonal to get the product, 5250. Start with the ones-place value and work towards the last-place value. Carry numbers to the next column if it is required.
Lattice Multiplication
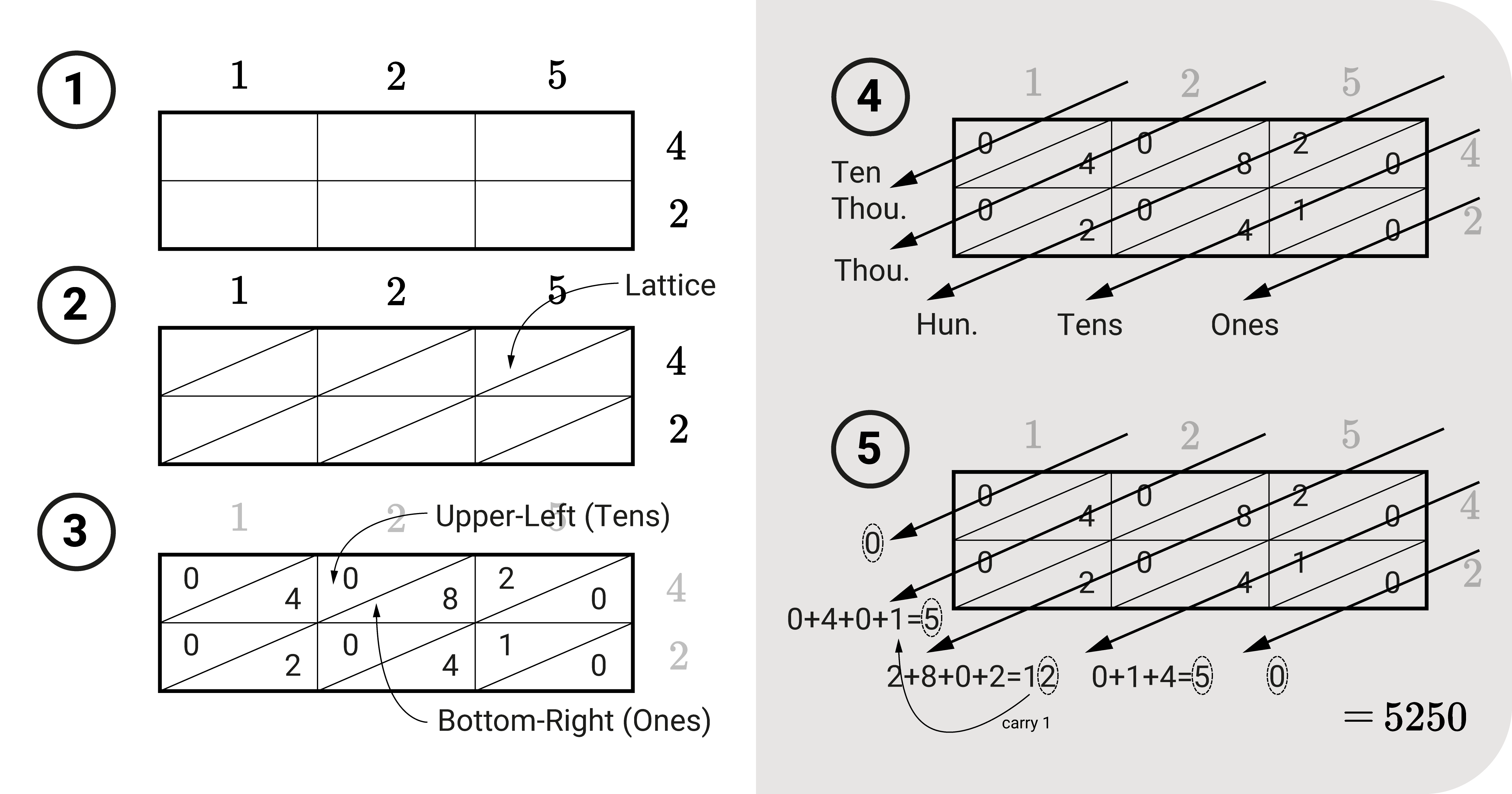
If you don't want to use sticks but have a similar approach is lattice multiplication
- Firstly, break down the multiplicand and multiplier into numbers and create a grid similar to what we've discussed with the stick method.
- Draw diagonals in every grid cell. Doing this will form a lattice, as shown in the figure.
- Multiply each row and column and place the product in the intersection cell. Since we have divided the cell into two using a diagonal, the upper-left portion will be the tens place while the bottom-right will be the ones place. To illustrate, let's consider the last column and the first row: 5 x 4 = 20. We place the "2" of 20 on the upper-left (since it's in the tens place) and the "0" on the bottom-right (since it's the ones place).
- Imagine a diagonal that runs through between the diagonals of the cell. Doing this will group numbers - see illustration to visualize it. These diagonals represent the place values of the final product (ones, tens, hundreds, and so on).
- Add the numbers per diagonal. Start from the ones-place value. Carry numbers to the next place if needed. The sum of the digits for each diagonal will read the product of the multiplicand and the multiplier, 5250.
Trachtenberg System
Another way of multiplying numbers is using the Trachtenberg system. It's a technique to do multiplication super fast mentally. It consists of a series of rules depending on the multiplier, which deserves a separate post.




