When solving structures, a grid reference (datum) is necessary to identify critical points. It's a concept often overlooked but essential if we want a uniform understanding of all structures.
Datum References
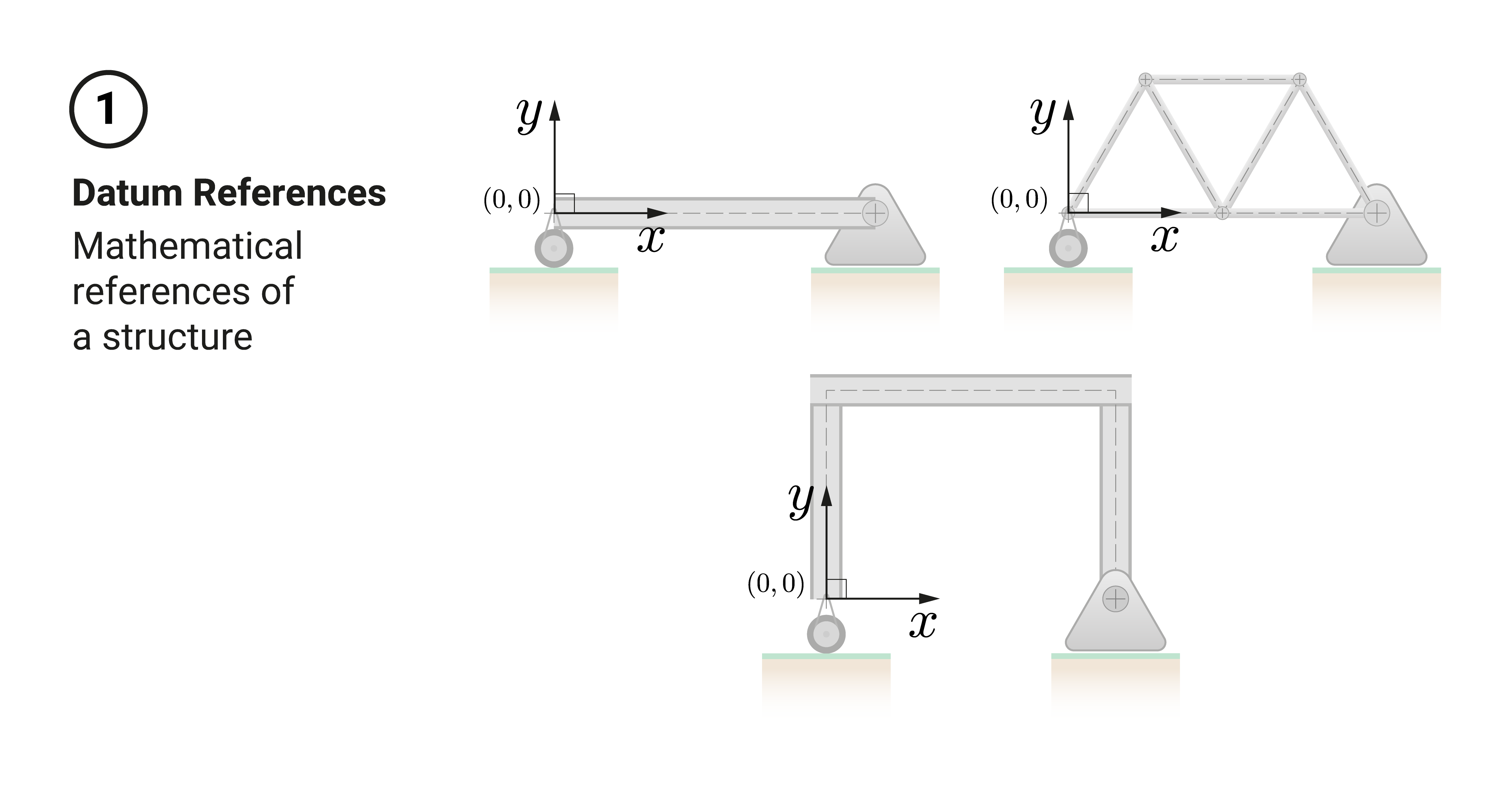
The most common way to establish references is the Cartesian grid reference. When using this system, we generally consider the following:
- We place the origin \(\left(0,0\right)\), usually at the bottom-left point of the structure.
- The x-axis runs horizontally through the origin, while the y-axis runs through the origin perpendicular to the x-axis.
In this way, all values are in Quadrant 1 (all are positive).
Global and Local References
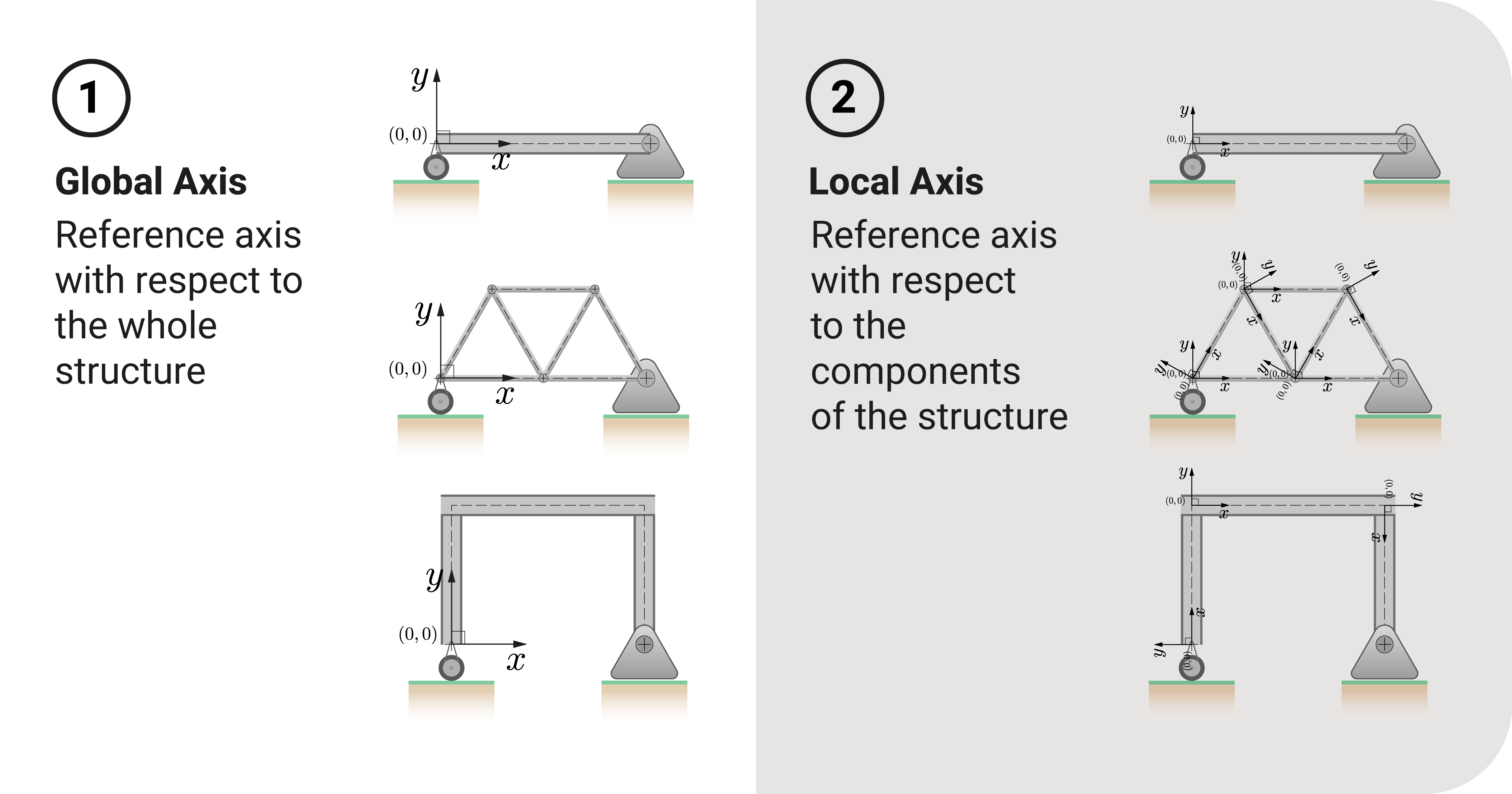
There are two types of references: global and local. The difference lies in how we see the structure as a whole.
To illustrate, let's consider a rigid plane frame \(ABCD\).
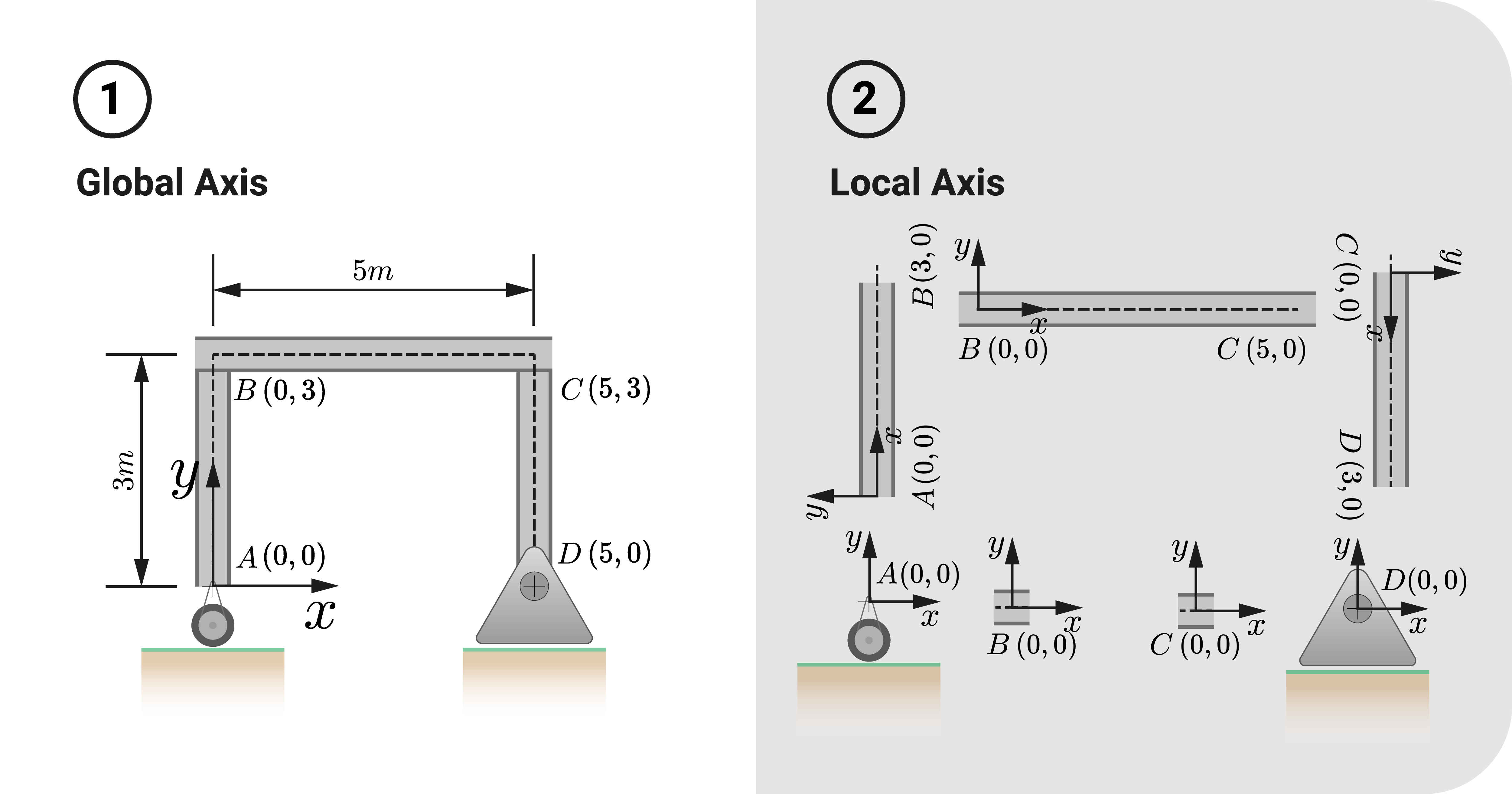
When we analyze a structure globally, we interpret it as a whole. It typically means that the origin is at the bottom-left point of the structure. In this case, it would be at point \(A\).
From origin \(A\), we can properly identify the location of other joints \(B\), \(C\), and \(D\) relative to point \(A\). Usually, we use this type to solve for the reaction supports in the classical method (more on structural analysis).
When we analyze a structure using local references, we break it into its elements and establish the datum per component.
In our rigid frame example, let's break it into members \(AB\), \(BC\), \(CD\), and joints \(A\), \(B\), \(C\), \(D\). After breaking it into its components, we can create our local reference for each. For example:
- In member \(AB\), we let the origin be at \(A\), and the x-axis goes from \(A\) to \(B\)
- In member \(BC\), we let the origin be at \(B\), and the x-axis goes from \(B\) to \(C\)
- In member \(CD\), we let the origin be at \(C\), and the x-axis goes from \(C\) to \(D\)
- In joint \(A\), we let the origin be at \(A\), and the y-axis parallel with member \(AB\)
- In joint \(B\), we let the origin be at \(B\), and the x-axis parallel with member \(BC\)
- In joint \(C\), we let the origin be at \(C\), and the x-axis parallel with member \(BC\)
- In joint \(D\), we let the origin be at \(D\), and the y-axis parallel with member \(CD\)
These references are limited to the components of the structure; hence, they're named "local." These are beneficial when we want to analyze the forces, stresses, and deflection per member.
Summary
Let's summarize:
Placing a grid reference to identify critical points is necessary when solving structures.
The most common way to establish one is the Cartesian grid reference.
There are two types: global and local.
When we analyze globally, we interpret the structure as a whole.
When we analyze locally, we break a structure into its elements and establish the datum per component.







