Let's recall that a function is an "input-output expression." We put something into it, and something comes out of it. Depending on the situation, we can have as many inputs as we can place. There are also other situations where we only limit the number of inputs.
Two Types of Domain
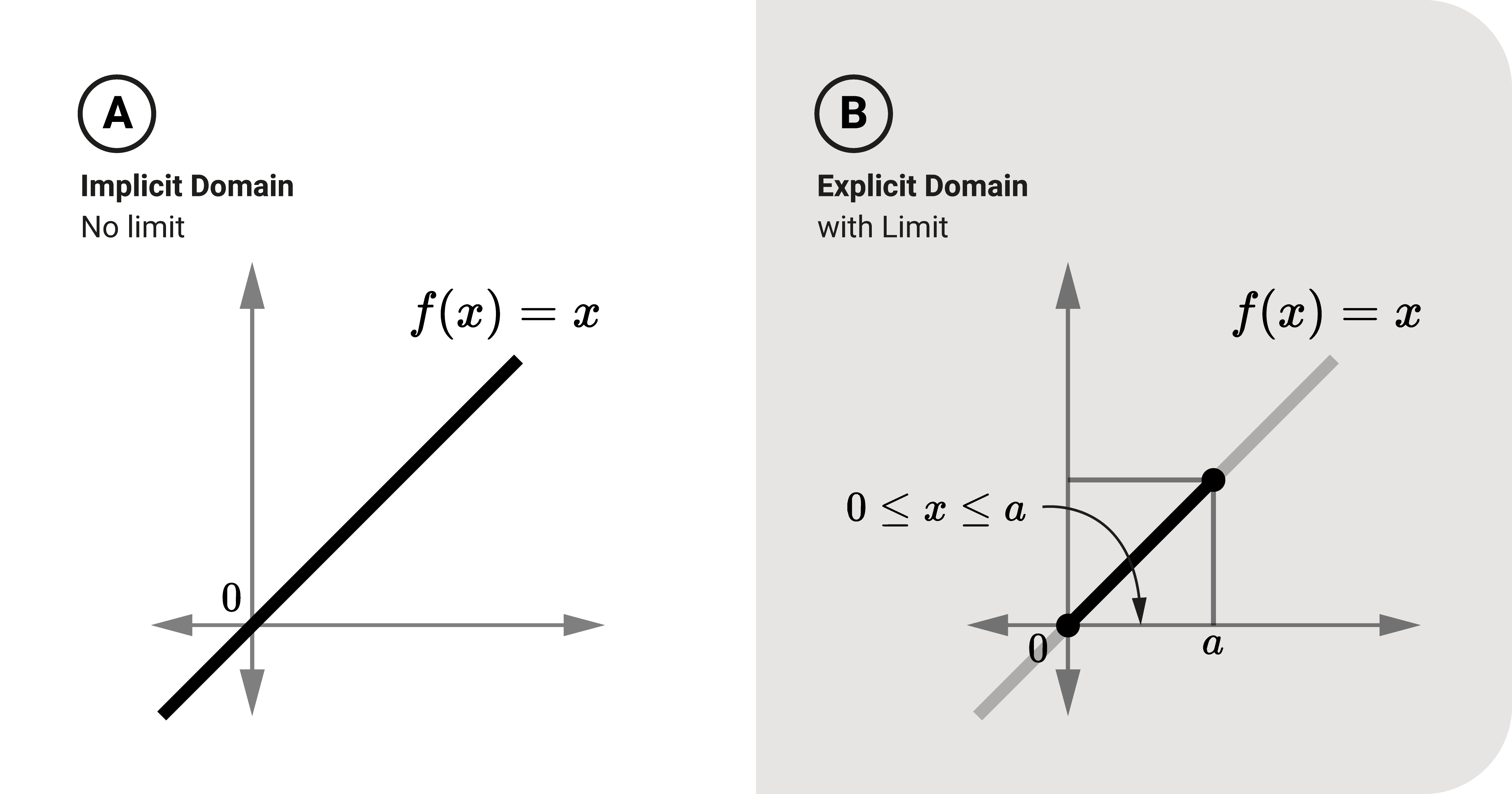
When it comes to functions, it's essential to define the domain, which can be (1) implicit or (2) explicit.
Mathematically, an implicit domain means the input is the set of all inputs, while an explicit means that it is limited based on some criteria.
To illustrate this, let's look at the radius r-area function: \(A(r)=\pi{r^2}\).
- The domain is the set of all possible values for the radius.
- Radii can only be a positive number (not less than zero). It usually doesn't make sense if we have a negative radius.
- As a result, we can further expand the function as \(A(r)=\pi{r^2}\), where \(r\geq0\).
If a condition like \(r\geq0\) exists, we have defined the domain, making it explicit.
However, if there is no stated condition in the function, then it is implied that the domain can be any real mathematical number. As a result, the domain is implicit.
When we have an explicitly-defined domain, the range will also limit itself. Returning to the radius-area example, we will only have positive areas as an output if we have only positive radii as inputs.
Summary
Domains can either be implicitly or explicitly defined.
An implicit domain means the input is the set of all inputs, while an explicit means that it is limited based on some criteria.







