Structures are deformable objects - they will change shape when applied with loads. When deformable objects experience such forces, a Strength of Materials course will tell you that it will develop stresses and strains.
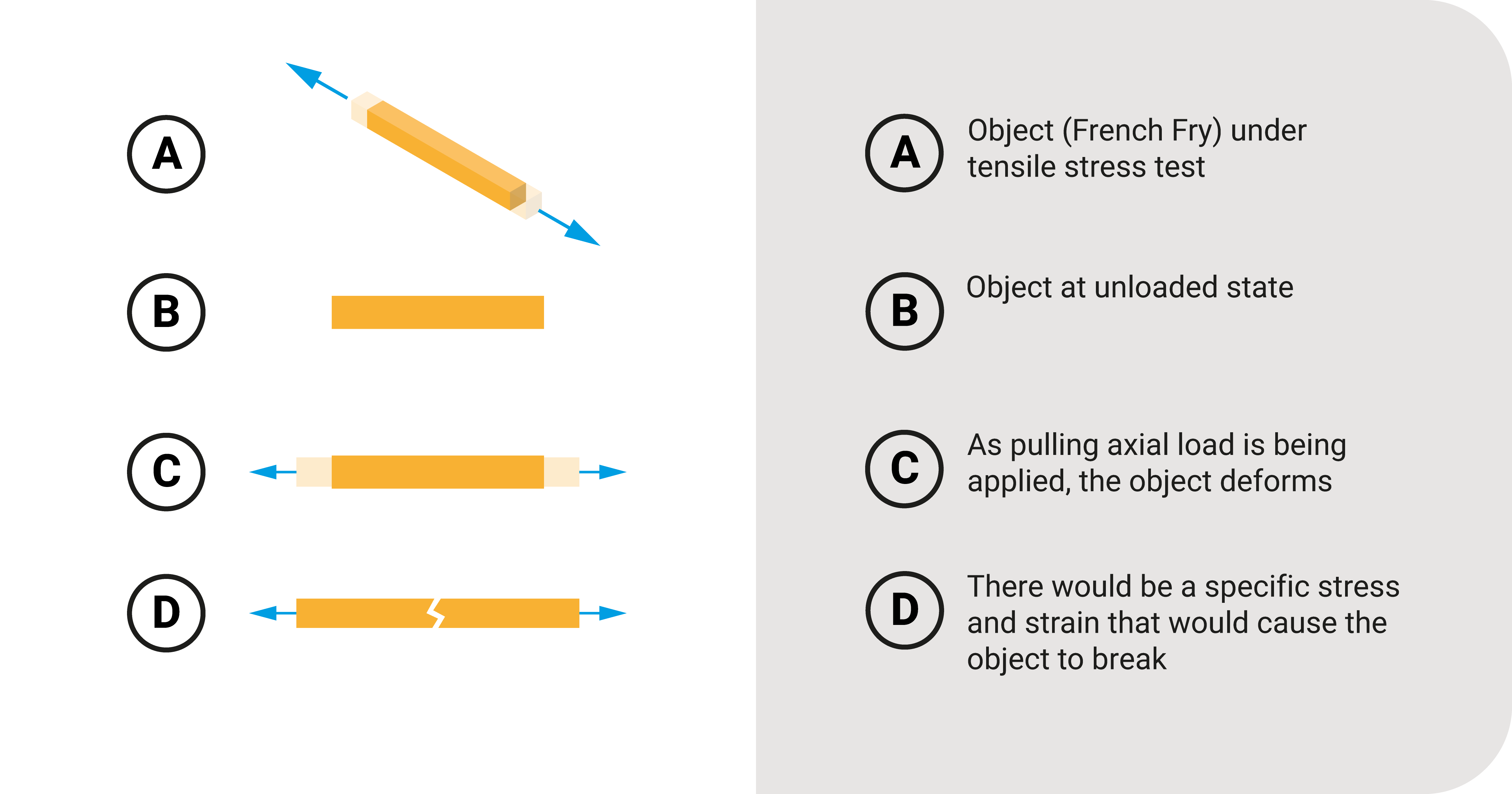
Let's consider a piece of French fry and pull it at both ends. What happens? It would elongate first, then break at a certain point if you pull it too hard. When you applied such force, the French fry experienced internal axial stress and strain that caused it to elongate.
This example reveals to us that there is a relationship between external loads and internal stresses and strains.
What are Constitutive Equations?
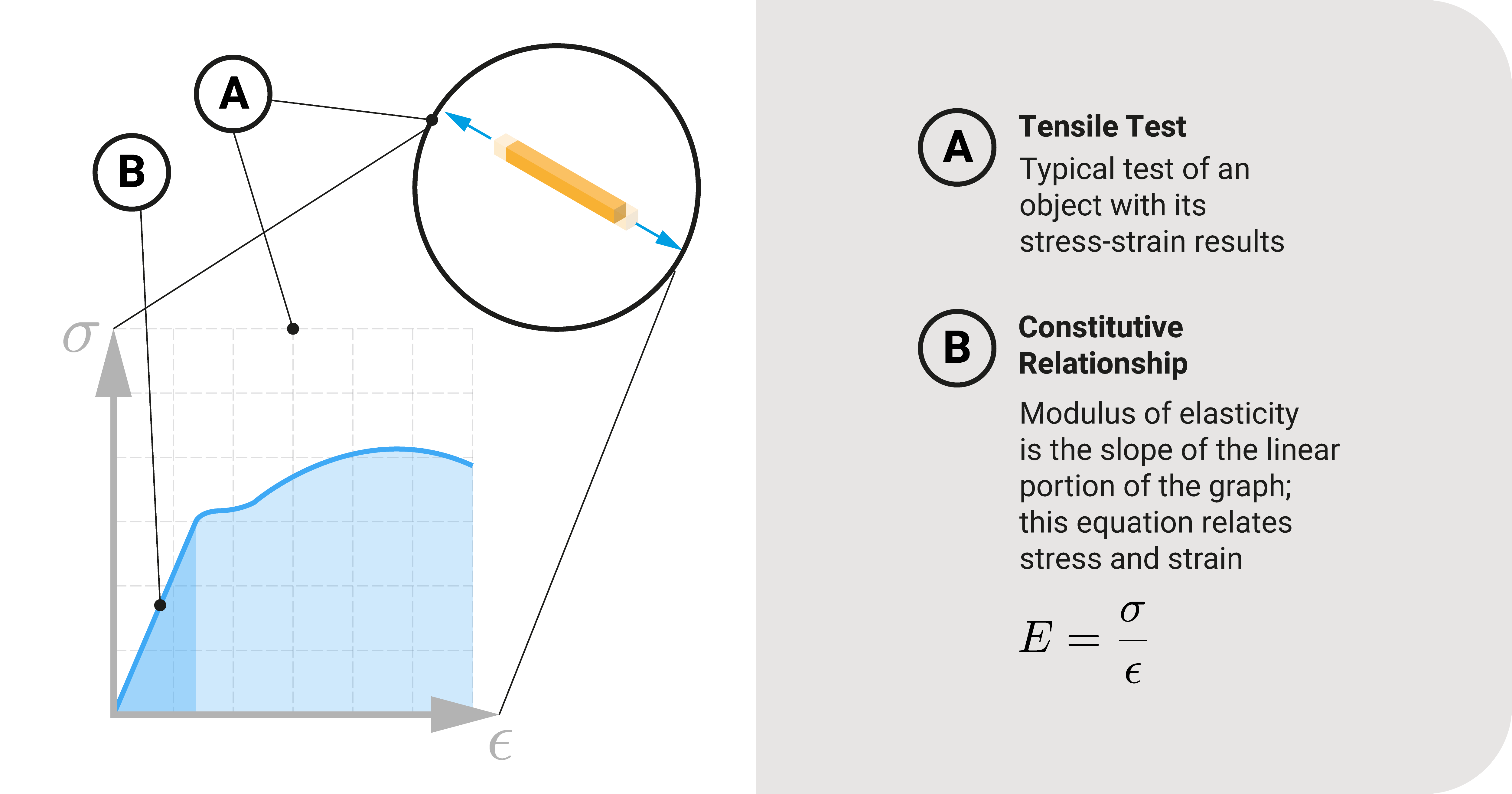
Constitutive equations, in structural analysis, tell us the relationship between loads and stresses to deformations and strains. It is the linchpin between these two quantities.
Let's consider the French fry example again (or any object). How do we relate the developed stress due to the pulling force to its strain?
If the deformation is elastic, one constitutive equation we could use would be the expression for Young's Modulus: \(E=\frac{{\sigma}}{{\epsilon}}\). Here, \({\sigma}\) is axial stress and \({\epsilon}\) is axial strain.
Constitutive relationships can be straightforward, as in our example, or complex. These expressions depend on the structure's size, shape, and material. It also varies based on the type of stress it is experiencing, whether it would be axial, shear, flexural, or torsional.
Summary
Constitutive equations tell us the relationship between loads and stresses to deformations and strains.





