One fascinating behavior of the cantilever beam is that we can observe a striking pattern when analyzing its moment diagram. At the end of this post, we shall have expressions that help us get the area and centroid of moment diagrams - a helpful skill in later structural topics.
Say we have a series of cantilever beams with different loading conditions:
- A couple at the free end
- A concentrated point load at the free end
- A uniform distributed load from 0 to \(L\)
- A uniform varying load from 0 to \(L\) (with the highest magnitude at the fixed support)
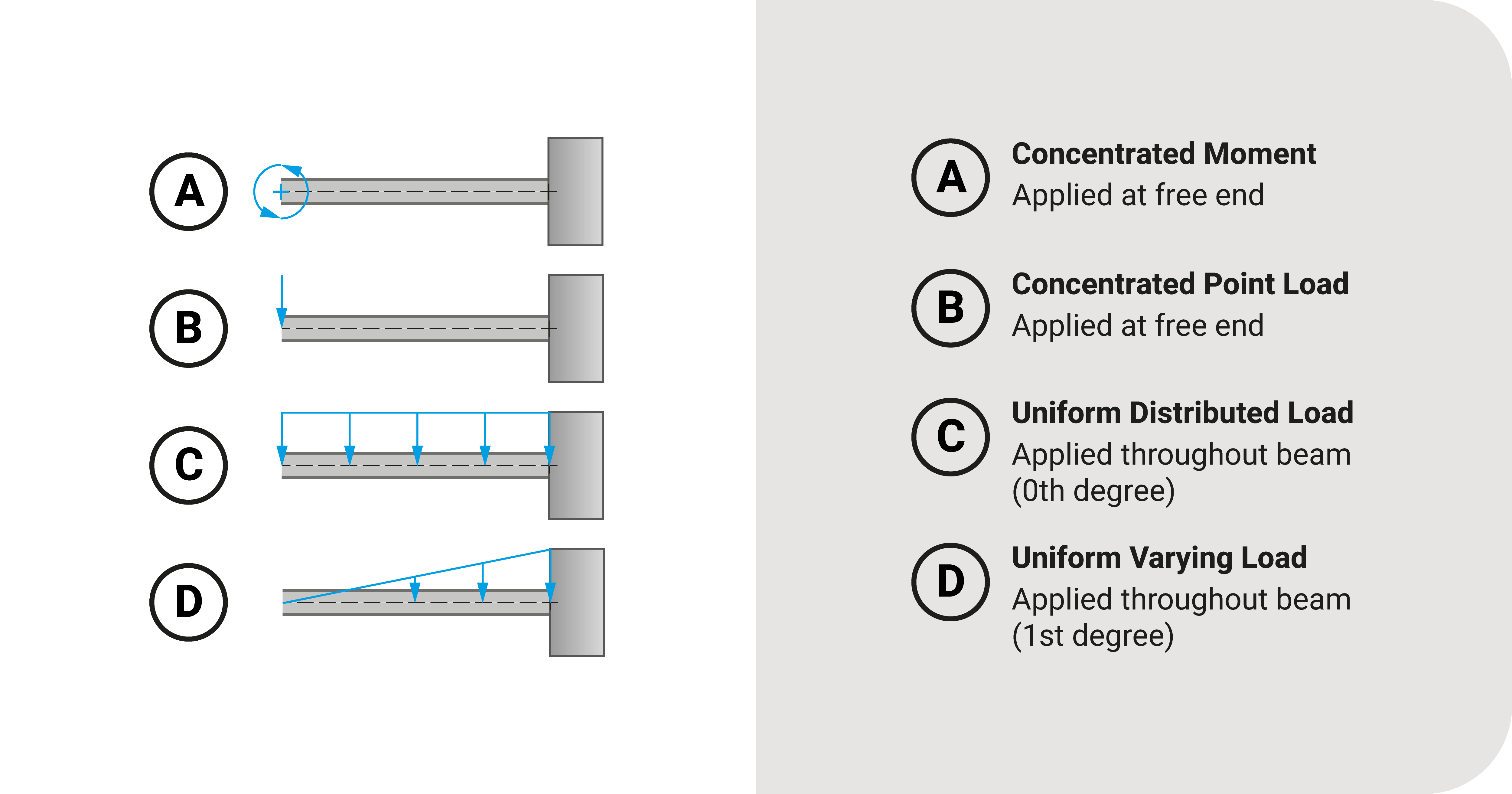
Let's analyze the moment expressions of these beams.
Moment Equations
Below is a table of the cantilever beams with different loading conditions. It shows their respective moment equations.
From this table, we can point out one key observation: the moment equations are polynomial functions of the form:
\(M=kx^n\)
- \(M\) is the internal bending moment at position \(x\).
- \(k\) is a constant depending on the loads.
- \(x\) is the position of the cutting plane section.
- \(n\) is the degree of the moment equation.
The degree \(n\) of the moment equation is an important variable and is the key to all cantilever patterns of such loading conditions.
Notice that the degree increases by one for each subsequent loading condition. If we're dealing with a couple, for example, the degree of the moment equation is zero. With a concentrated point load, the degree is one.



